题目内容
(2013•盐城三模)将一张长8cm,宽6cm的长方形的纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1cm2,S2cm2,其中S1≤S2.记折痕长为lcm.
(1)若l=4,求S1的最大值;
(2)若S1:S2=1:2,求l的取值范围.
(1)若l=4,求S1的最大值;
(2)若S1:S2=1:2,求l的取值范围.
分析:(1)不妨设纸片为长方形ABCD,AB=8cm,AD=6cm,其中点A在面积为S1的部分内.折痕有下列三种情形:①折痕的端点M,N分别在边AB,AD上;②折痕的端点M,N分别在边AB,CD上;③折痕的端点M,N分别在边AD,BC上.易判断l=4为情形①,设AM=xcm,AN=ycm,则x2+y2=16.利用不等式即可求得S1的最大值;
(2)由题意知,长方形的面积为S=6×8=48,因为S1:S2=1:2,S1≤S2,所以S1=16,S2=32,按三种情形进行讨论:根据S1的面积可把折痕l表示为函数,根据函数的特点可用导数或二次函数性质分别求得l的范围,综上即可求得l的范围;
(2)由题意知,长方形的面积为S=6×8=48,因为S1:S2=1:2,S1≤S2,所以S1=16,S2=32,按三种情形进行讨论:根据S1的面积可把折痕l表示为函数,根据函数的特点可用导数或二次函数性质分别求得l的范围,综上即可求得l的范围;
解答:解:如图所示:不妨设纸片为长方形ABCD,AB=8cm,AD=6cm,其中点A在面积为S1的部分内.折痕有下列三种情形:
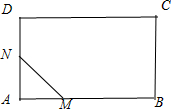
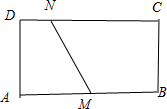
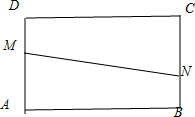
情形①情形②情形③
①折痕的端点M,N分别在边AB,AD上;
②折痕的端点M,N分别在边AB,CD上;
③折痕的端点M,N分别在边AD,BC上.
(1)在情形②③中,MN≥6,故当l=4时,折痕必定是情形①.
设AM=xcm,AN=ycm,则x2+y2=16.
因为x2+y2≥2xy,当且仅当x=y时取等号,
所以S1=
xy≤4,当且仅当x=y=2
时取等号,即S1的最大值为4.
(2)由题意知,长方形的面积为S=6×8=48,
因为S1:S2=1:2,S1≤S2,所以S1=16,S2=32.
当折痕是情形①时,设AM=xcm,AN=ycm,则
xy=16,即y=
,
由
,解得
≤x≤8,
所以l=
=
,
≤x≤8,
设f(x)=x2+
,x>0,则f′(x)=2x-
=
,x>0,
故当x∈(
,4
)时f′(x)<0,f(x)递减,当x∈(4
,8)时,f′(x)>0,f(x)递增,且f(
)=64
,f(8)=80,
所以f(x)的取值范围为[64,80],从而l的范围是[8,4
].
当折痕是情形②时,设AM=xcm,DN=ycm,则
(x+y)×6=16,即y=
-x,
由
,解得0≤x≤
,
所以l=
=
,0≤x≤
,
所以l的范围为[6,
];
当折痕是情形③时,设BN=xcm,AM=ycm,则
(x+y)×8=16,即y=4-x,
由
,得0≤x≤4,所以l=
=
,0≤x≤4,
所以l的取值范围为[8,4
],
综上,l的取值范围为[6,4
].

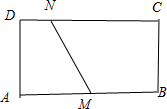

情形①情形②情形③
①折痕的端点M,N分别在边AB,AD上;
②折痕的端点M,N分别在边AB,CD上;
③折痕的端点M,N分别在边AD,BC上.
(1)在情形②③中,MN≥6,故当l=4时,折痕必定是情形①.
设AM=xcm,AN=ycm,则x2+y2=16.
因为x2+y2≥2xy,当且仅当x=y时取等号,
所以S1=
| 1 |
| 2 |
| 2 |
(2)由题意知,长方形的面积为S=6×8=48,
因为S1:S2=1:2,S1≤S2,所以S1=16,S2=32.
当折痕是情形①时,设AM=xcm,AN=ycm,则
| 1 |
| 2 |
| 32 |
| x |
由
|
| 16 |
| 3 |
所以l=
| x2+y2 |
x2+
|
| 16 |
| 3 |
设f(x)=x2+
| 322 |
| x2 |
| 2×322 |
| x3 |
2(x2+32)(x+4
| ||||
| x3 |
故当x∈(
| 16 |
| 3 |
| 2 |
| 2 |
| 16 |
| 3 |
| 4 |
| 9 |
所以f(x)的取值范围为[64,80],从而l的范围是[8,4
| 5 |
当折痕是情形②时,设AM=xcm,DN=ycm,则
| 1 |
| 2 |
| 16 |
| 3 |
由
|
| 16 |
| 3 |
所以l=
| 62+(x-y)2 |
62+4(x-
|
| 16 |
| 3 |
所以l的范围为[6,
2
| ||
| 3 |
当折痕是情形③时,设BN=xcm,AM=ycm,则
| 1 |
| 2 |
由
|
| 82+(x-y)2 |
| 82+4(x-2)2 |
所以l的取值范围为[8,4
| 5 |
综上,l的取值范围为[6,4
| 5 |
点评:本题考查利用导数、不等式求函数的最值,考查分类讨论思想、函数思想、数形结合思想,考查学生分析解决问题的能力.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 (2013•盐城三模)已知函数f (x)=2sin(ωx+?)(ω>0)的部分图象如图所示,则ω=
(2013•盐城三模)已知函数f (x)=2sin(ωx+?)(ω>0)的部分图象如图所示,则ω=