题目内容
（13分）已知各项均为正数的数列{
n }的前n项和Sn满足S1>1，
且6Sn=(n +1)(n +2) (n为正整数）。（1）求{n}的通项公式；
（2）设数列{bn}满足bn=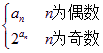
，求Tn=b1+ b2+…+bn；
（1）an=3n-1（2）Tn=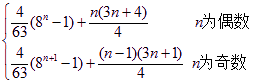
解析:
（1）n=1时，6a1=
且a1>1，∴a1=2
当n≥2时，由an=Sn-Sn-1得，6an=
∴（an+an-1）（an-an-1-3）=0，又an>0(n∈N*)，∴an-an-1=3，
从而{an}为等差数列，an=3n-1
（2）依题bn=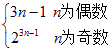
，
当n为偶数时，Tn=(b1+b3+…+bn-1)+(b2+b4+…+bn)=…
当n为奇数时，Tn=(b1+b3+…+bn)+(b2+b4+…+bn-1)=…
∴Tn=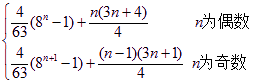
练习册系列答案
相关题目
与
的大小，并加以证明．
与
的大小，并加以证明．
与
的大小，并加以证明．