题目内容
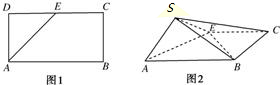
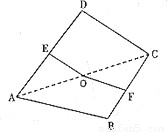
如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列说法中正确的有
①存在点E使得直线SA⊥平面SBC;
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行;
④存在点E使得SE⊥BA.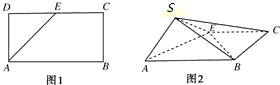
- A.1个
- B.2个
- C.3个
- D.4个
A
分析:由已知中点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,我们可得∠SAD为锐角,∠SEC为钝角,逐一分析题目中的四个结论,分别分析出它们的真假,即可得到答案.
解答:①若直线SA⊥平面SBC,
则直线SA与平面SBC均垂直,则SA⊥BC,
又由AD∥BC,则SA⊥AD,这与∠SAD为锐角矛盾,故①错误;
②∵平面SBC∩直线SA=S,
故平面SBC内的直线与SA相交或异面,故②错误;
③取AB的中点F,则CF∥AE,由线面平行的判定定理,可得CF∥SAE平行,故③正确;
④若SE⊥BA,由EC∥AB,可得SE⊥EC,这与∠SEC为钝角矛盾,故④错误;
故选A.
点评:本题考查的知识点是平面与平面垂直的性质,反证法,其中根据对于存在性结论的论证,从正面论证难度较大时,一般使用反证法来进行证明.
分析:由已知中点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,我们可得∠SAD为锐角,∠SEC为钝角,逐一分析题目中的四个结论,分别分析出它们的真假,即可得到答案.
解答:①若直线SA⊥平面SBC,
则直线SA与平面SBC均垂直,则SA⊥BC,
又由AD∥BC,则SA⊥AD,这与∠SAD为锐角矛盾,故①错误;
②∵平面SBC∩直线SA=S,
故平面SBC内的直线与SA相交或异面,故②错误;
③取AB的中点F,则CF∥AE,由线面平行的判定定理,可得CF∥SAE平行,故③正确;
④若SE⊥BA,由EC∥AB,可得SE⊥EC,这与∠SEC为钝角矛盾,故④错误;
故选A.
点评:本题考查的知识点是平面与平面垂直的性质,反证法,其中根据对于存在性结论的论证,从正面论证难度较大时,一般使用反证法来进行证明.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
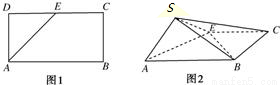
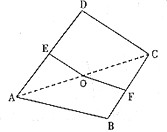 如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )
如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )| A、30° | B、60° | C、120° | D、150° |