题目内容
(本小题满分15分)
定义在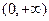 上的函数
上的函数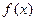 满足
满足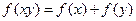 ,且当
,且当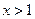 时,
时,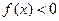 .
.
(1)求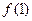 ;
;
(2)证明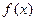 在
在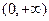 上单调递减;
上单调递减;
(3)若关于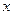 的不等式
的不等式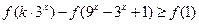 恒成立,求实数
恒成立,求实数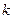 的取值范围.
的取值范围.
定义在
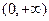 上的函数
上的函数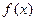 满足
满足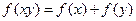 ,且当
,且当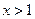 时,
时,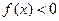 .
.(1)求
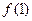 ;
; (2)证明
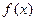 在
在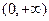 上单调递减;
上单调递减;(3)若关于
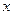 的不等式
的不等式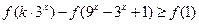 恒成立,求实数
恒成立,求实数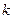 的取值范围.
的取值范围.(1)0
(2)证明略
(3)

(1)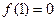 ; ………………(5分)
; ………………(5分)
(2)由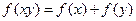 可得
可得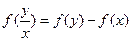 ,
,
设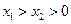 ,
,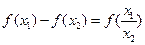 ,
,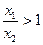 ,
,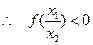 ,即
,即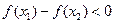
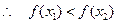 ,所以
,所以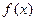 在
在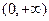 上单调递减;…………(10分)
上单调递减;…………(10分)
(3)因为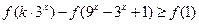 ,所以
,所以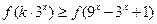 ,
,
由(2)得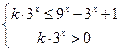 (*)恒成立,令
(*)恒成立,令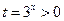 ,
,
则(*)可化为 对任意
对任意 恒成立,且
恒成立,且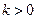 ,
,

 .……………(15分)
.……………(15分)
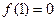 ; ………………(5分)
; ………………(5分)(2)由
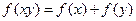 可得
可得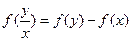 ,
,设
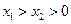 ,
,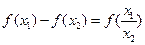 ,
,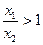 ,
,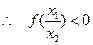 ,即
,即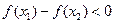
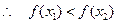 ,所以
,所以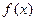 在
在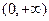 上单调递减;…………(10分)
上单调递减;…………(10分)(3)因为
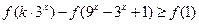 ,所以
,所以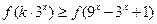 ,
,由(2)得
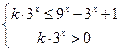 (*)恒成立,令
(*)恒成立,令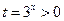 ,
,则(*)可化为
 对任意
对任意 恒成立,且
恒成立,且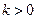 ,
,
 .……………(15分)
.……………(15分)
练习册系列答案
相关题目
 ,则给出下列四个命题:①函数
,则给出下列四个命题:①函数 的定义域是R,值域为[0,1];②方程
的定义域是R,值域为[0,1];②方程 有无数个解;③函数
有无数个解;③函数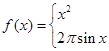
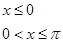 ,则集合
,则集合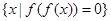 中元素的个数有 ( )
中元素的个数有 ( )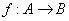 ,其中
,其中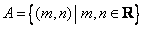 ,
,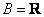 . 已知对所有的有序正整数对
. 已知对所有的有序正整数对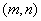 满足下述条件:①
满足下述条件:①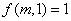 ;②若
;②若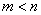 ,
,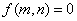 ; ③
; ③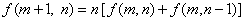 . 则
. 则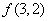 的值是___________;
的值是___________;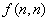 的表达式为___________。(用含
的表达式为___________。(用含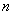 的代数式表示)。
的代数式表示)。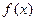 的定义域为
的定义域为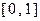 ,且同时满足:①
,且同时满足:①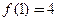 ;②若
;②若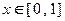 ,都有
,都有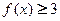 ;③若
;③若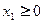 ,
,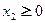 ,
,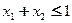 ,都有
,都有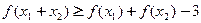 .
.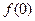 的值;
的值;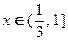 时,求证:
时,求证: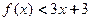 .
.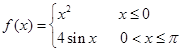 则集合
则集合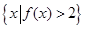 等于 ( )
等于 ( )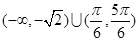



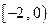 ∪
∪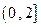 上的奇函数,当
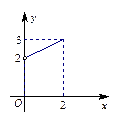
上的奇函数,当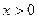 时,f (x)的图象如右图所示,那么f (x)的值域是
时,f (x)的图象如右图所示,那么f (x)的值域是 

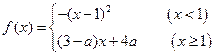 满足对任意
满足对任意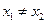 都有
都有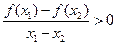 成立,则a的取值范围是 ▲ .
成立,则a的取值范围是 ▲ . 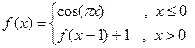 ,则
,则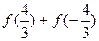 的值是____
的值是____