题目内容
已知函数f(x)=alnx-ax-3(a∈R),
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数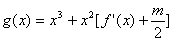 在区间(t,3)上总不是单调函数,求m的取值范围;
在区间(t,3)上总不是单调函数,求m的取值范围;
(3)求证: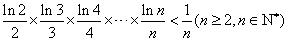 。
。
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数
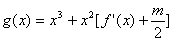 在区间(t,3)上总不是单调函数,求m的取值范围;
在区间(t,3)上总不是单调函数,求m的取值范围;(3)求证:
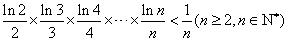 。
。 (1)解: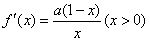 ,
,
当a>0时,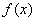 的单调增区间为
的单调增区间为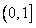 ,减区间为
,减区间为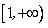 ;
;
当a<0时,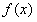 的单调增区间为
的单调增区间为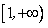 ,减区间为
,减区间为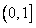 ;
;
当a=0时,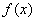 不是单调函数。
不是单调函数。
(2)解: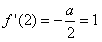 ,∴
,∴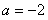 ,
,
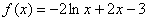 ,
,
∴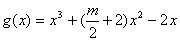 ,
,
∴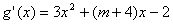 ,
,
∵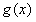 在区间(t,3)上总不是单调函数,且
在区间(t,3)上总不是单调函数,且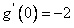 ,
,
∴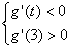 ,
,
由题意知:对于任意的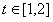 ,
,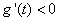 恒成立,
恒成立,
所以,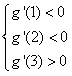 ,∴
,∴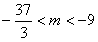 ,
,
所以,m的取值范围是(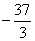 ,-9)。
,-9)。
(3)证明:令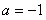 ,此时
,此时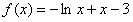 ,
,
所以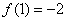 ,
,
由(1)知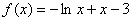 在
在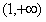 上单调递增,
上单调递增,
∴当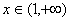 时,
时,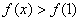 ,
,
即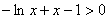 ,
,
∴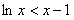 ,对一切
,对一切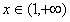 成立,
成立,
∵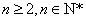 ,
,
则有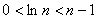 ,
,
∴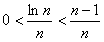 ,
,
∴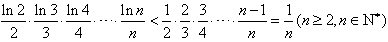 。
。
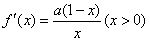 ,
,当a>0时,
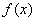 的单调增区间为
的单调增区间为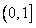 ,减区间为
,减区间为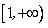 ;
;当a<0时,
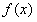 的单调增区间为
的单调增区间为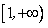 ,减区间为
,减区间为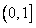 ;
;当a=0时,
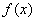 不是单调函数。
不是单调函数。(2)解:
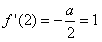 ,∴
,∴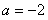 ,
,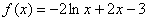 ,
,∴
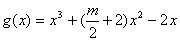 ,
,∴
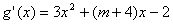 ,
,∵
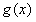 在区间(t,3)上总不是单调函数,且
在区间(t,3)上总不是单调函数,且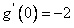 ,
,∴
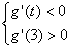 ,
,由题意知:对于任意的
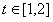 ,
,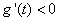 恒成立,
恒成立, 所以,
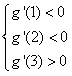 ,∴
,∴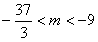 ,
,所以,m的取值范围是(
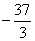 ,-9)。
,-9)。(3)证明:令
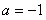 ,此时
,此时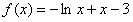 ,
,所以
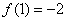 ,
,由(1)知
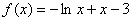 在
在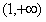 上单调递增,
上单调递增,∴当
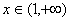 时,
时,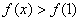 ,
,即
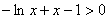 ,
,∴
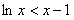 ,对一切
,对一切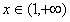 成立,
成立,∵
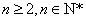 ,
,则有
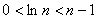 ,
,∴
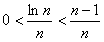 ,
,∴
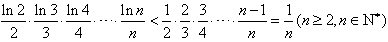 。
。
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目