题目内容
【题目】已知![]() ,
,![]() 是实数,函数
是实数,函数![]() ,
,![]() ,若
,若![]() 在区间
在区间![]() 上恒成立,则称
上恒成立,则称![]() 和
和![]() 在区间
在区间![]() 上为“
上为“![]() 函数”.
函数”.
(1)设![]() ,若
,若![]() 和
和![]() 在区间
在区间![]() 上为“
上为“![]() 函数”,求实数
函数”,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() 且
且![]() ,若
,若![]() 和
和![]() 在以
在以![]() ,
,![]() 为端点的开区间上为“
为端点的开区间上为“![]() 函数”,求
函数”,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)按照“![]() 函数”的定义,将函数表达式代入
函数”的定义,将函数表达式代入![]() ,化简得
,化简得![]() ,所以有
,所以有![]() ,解得
,解得![]() ;(2)分别按
;(2)分别按![]() ,
,![]() 两类,结合“
两类,结合“![]() 函数”的定义,类似(1)的方法,讨论得
函数”的定义,类似(1)的方法,讨论得![]() 的最大值为
的最大值为![]() .
.
试题解析:
(1)因为![]() 和
和![]() 在区间
在区间![]() 上为“
上为“![]() 函数”,
函数”,
所以![]() ,在
,在![]() 上恒成立,
上恒成立,
即![]() ,
,![]()
![]() ,
,![]()
![]() ,即
,即![]() ,
,![]() ,
,![]() .……………(4分)
.……………(4分)
(2)①当![]() 时,因为
时,因为![]() 和
和![]() 在以
在以![]() ,
,![]() 为端点的开区间上为“
为端点的开区间上为“![]() 函数”,
函数”,
所以,![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,
,![]() 恒成立,
恒成立,
![]() ,
,![]() 对任意
对任意![]() ,
,![]() ,
,
故对任意![]() ,
,![]() ,
,
![]() ,
,
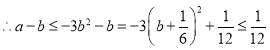 .………………(8分)
.………………(8分)
②当![]() 时,因为
时,因为![]() 和
和![]() 在以
在以![]() ,
,![]() 为端点的开区间上为“
为端点的开区间上为“![]() 函数”,所以
函数”,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,
,![]() 恒成立,
恒成立,
![]() ,
,![]() 对任意
对任意![]() ,
,![]() ,
,
故对任意![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
综上可知,![]() .……………………………(12分)
.……………………………(12分)

练习册系列答案
相关题目

