题目内容

精英家教网已知函数y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜π）的图象如图所示，则该函数的解析式是（　　）
A、y=2sin(
2
7
x+
π
6
)
B、y=2sin(-
2
7
x+
7π
6
)
C、y=2sin(2x+
π
6
)
D、y=2sin(2x-
π
6
)
分析：由已知，可以看出A=2，周期不能直接看出，但估算到
T
2
＜
7π
12
，得出ω＞
12
7
，再结合特殊点（0，1）去求解．
解答：解：由图象可以看出A=2，把（0，1）代入各解析式，排除B，D，又
T
2
＜
7π
12
，得出ω＞
12
7
，故只有C符合．
故选C．
点评：本题考查由y=Asin（ωx+φ）部分图象确定其解析式，选择题，可有排除法，第一步，代入特殊点，第二步，求周期范围．
练习册系列答案
相关题目
已知函数y=Asin（ωx+φ），在同一周期内，当x=
π
12
时，取最大值y=2，当x=
7π
12
时，取得最小值y=-2，那么函数的解析式为（　　）
A、y=
1
2
sin（x+
π
3
）
B、y=2sin（2x+
π
3
）
C、y=2sin（
x
2
-
π
6
）
D、y=2sin（2x+
π
6
）
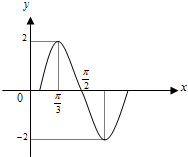精英家教网已知函数y=Asin（ωx+∅）（A＞0，ω＞0，-π≤∅≤π）一个周期的图象（如图），则这个函数的一个解析式为（　　）
A、y=2sin(
3
2
x+
π
2
)
B、y=2sin(3x+
π
6
)
C、y=2sin(3x-
π
6
)
D、y=2sin(3x-
π
2
)
已知函数y=Asin(ωx+?)+B(A＞0，ω＞0，|?|＜
π
2
)的周期为T，在一个周期内的图象如图所示，则φ=
-
π
6
-
π
6
．
已知函数y=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)的一部分图象如图所示，则（　　）
已知函数y=Asin（ωx+∅）+k的最大值为4，最小值为0，最小正周期是
π
2
，在x∈[
π
24
，
π
12
]上单调递增，则下列符合条件的解析式是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网