题目内容
为了治理“沙尘暴”,西部某地区政府经过多年努力,到2009年底,将当地沙漠绿化了40%,从2010年开始,每年将出现这种现象:原有沙漠面积的12%被绿化,即改造为绿洲(被绿化的部分叫绿洲),同时原有绿洲面积的8%又被侵蚀为沙漠,问至少经过几年的绿化,才能使该地区的绿洲面积超过50%?(可参考数据lg2=0.3,最后结果精确到整数).
至少需要4年才能使绿化面积超过50%
设该地区总面积为1,2006年底绿化面积为a1=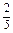 ,经过n年后绿洲面积为an+1,设2009年底沙漠面积为b1,经过n年后沙漠面积为bn+1,则a1+b1=1,an+bn=1.
,经过n年后绿洲面积为an+1,设2009年底沙漠面积为b1,经过n年后沙漠面积为bn+1,则a1+b1=1,an+bn=1.
依题意an+1由两部分组成:一部分是原有绿洲an减去被侵蚀的部分8%·an的剩余面积92%·an,另一部分是新绿化的12%·bn,所以
an+1=92%·an+12%(1-an)=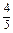 an+
an+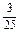 ,即an+1-
,即an+1-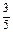 =
=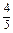 (an-
(an-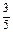 ),
),
∴ 是以-
是以-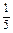 为首项,
为首项,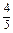 为公比的等比数列,
为公比的等比数列,
则an+1=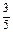 -
-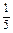
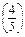 n,
n,
∵an+1>50%,∴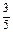 -
-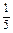
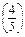 n>
n> ,
,
∴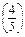 n﹤
n﹤ ,n>log
,n>log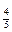
 =
= =3.
=3.
则当n≥4时,不等式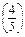 n﹤
n﹤ 恒成立.
恒成立.
所以至少需要4年才能使绿化面积超过50%.
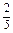 ,经过n年后绿洲面积为an+1,设2009年底沙漠面积为b1,经过n年后沙漠面积为bn+1,则a1+b1=1,an+bn=1.
,经过n年后绿洲面积为an+1,设2009年底沙漠面积为b1,经过n年后沙漠面积为bn+1,则a1+b1=1,an+bn=1.依题意an+1由两部分组成:一部分是原有绿洲an减去被侵蚀的部分8%·an的剩余面积92%·an,另一部分是新绿化的12%·bn,所以
an+1=92%·an+12%(1-an)=
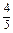 an+
an+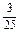 ,即an+1-
,即an+1-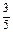 =
=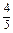 (an-
(an-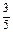 ),
),∴
 是以-
是以-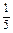 为首项,
为首项,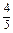 为公比的等比数列,
为公比的等比数列,则an+1=
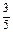 -
-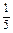
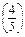 n,
n,∵an+1>50%,∴
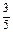 -
-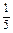
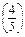 n>
n> ,
,∴
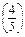 n﹤
n﹤ ,n>log
,n>log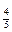
 =
= =3.
=3.则当n≥4时,不等式
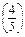 n﹤
n﹤ 恒成立.
恒成立.所以至少需要4年才能使绿化面积超过50%.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
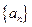 ,公比为
,公比为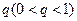 ,
,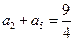 ,
,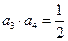 。
。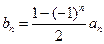 ,求证:
,求证: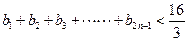 。
。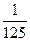 的最小整数n是 ( )
的最小整数n是 ( )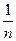 [lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.
[lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.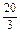 ,求{an}的通项公式.
,求{an}的通项公式. ,1,
,1, 成等差数列,实数a2,1,c2成等比数列,则
成等差数列,实数a2,1,c2成等比数列,则 =____________.
=____________. 各项为正数,
各项为正数, 是其前
是其前 项和,且
项和,且
 .
. 及
及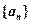 满足:
满足: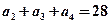 ,且
,且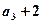 是
是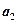 ,
,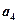 的等差中项,则数列
的等差中项,则数列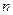 项和
项和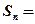 .
.