题目内容
已知函数f(x)=ex,g(x)=1+ax+ 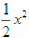 ,a∈R
,a∈R
(1)设函数F(x)=f(x)-g(x),讨论F(x)的极值点的个数;
(2)若-2≤a≤1,求证:对任意的x1,x2∈[1,2],且x1<x2时,都有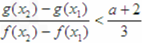
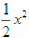 ,a∈R
,a∈R(1)设函数F(x)=f(x)-g(x),讨论F(x)的极值点的个数;
(2)若-2≤a≤1,求证:对任意的x1,x2∈[1,2],且x1<x2时,都有
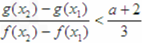
解:(1 )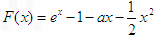 ,F'(x)=ex-a-x,F''(x)=ex-1,
,F'(x)=ex-a-x,F''(x)=ex-1,
令F''(x)=0,得x=0
当x∈(-∞,0)时,F''(x)<0,从而F'(x)在(- ∞,0)上单调递减,
当x∈(0,+ ∞)时, F''(x)>0,从而F'(x)在(0,+ ∞)上单调递增,
所以F'(x)min=F'(x)=1-a,
当F'(x)min=1-a≥0,即a≤1时,F'(x) ≥0恒成立,F(x)的极值点个数为0;
当F'(x)min=1-a<0,即a>1时,(又x→-∞,F'(x) →+∞, x→+∞,F'(x) →+∞)F(x)的极值点个数为2个
(2)证明: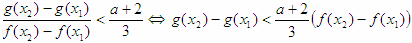
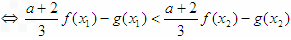
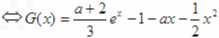 在[1,2]上单调递增
在[1,2]上单调递增
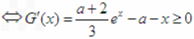 在x∈[1,2]上恒成立
在x∈[1,2]上恒成立
令H(a)=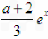 -a-x=
-a-x=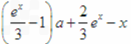 (-2≤a≤1),关于a是一次函数。
(-2≤a≤1),关于a是一次函数。
又H(-2)=2-x≥0,H(1)=ex-1-x≥0,(由F'(x)=ex-a-x≥1-a得)
所以G(x)=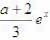 -a-x≥0在x∈[1,2]上恒成立,所以,原命题成立。
-a-x≥0在x∈[1,2]上恒成立,所以,原命题成立。
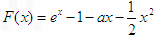 ,F'(x)=ex-a-x,F''(x)=ex-1,
,F'(x)=ex-a-x,F''(x)=ex-1,令F''(x)=0,得x=0
当x∈(-∞,0)时,F''(x)<0,从而F'(x)在(- ∞,0)上单调递减,
当x∈(0,+ ∞)时, F''(x)>0,从而F'(x)在(0,+ ∞)上单调递增,
所以F'(x)min=F'(x)=1-a,
当F'(x)min=1-a≥0,即a≤1时,F'(x) ≥0恒成立,F(x)的极值点个数为0;
当F'(x)min=1-a<0,即a>1时,(又x→-∞,F'(x) →+∞, x→+∞,F'(x) →+∞)F(x)的极值点个数为2个
(2)证明:
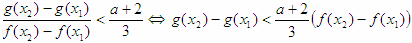
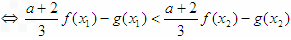
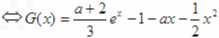 在[1,2]上单调递增
在[1,2]上单调递增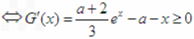 在x∈[1,2]上恒成立
在x∈[1,2]上恒成立令H(a)=
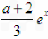 -a-x=
-a-x=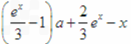 (-2≤a≤1),关于a是一次函数。
(-2≤a≤1),关于a是一次函数。又H(-2)=2-x≥0,H(1)=ex-1-x≥0,(由F'(x)=ex-a-x≥1-a得)
所以G(x)=
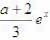 -a-x≥0在x∈[1,2]上恒成立,所以,原命题成立。
-a-x≥0在x∈[1,2]上恒成立,所以,原命题成立。
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目