题目内容
某校举办一场篮球投篮选拔比赛，比赛的规则如下：每个选手先后在二分区、三分区和中场跳球区三个位置各投一球，只有当前一次球投进后才能投下一次，三次全投进就算胜出，否则即被淘汰. 已知某选手在二分区投中球的概率为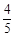
，在三分区投中球的概率为
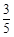，在中场跳球区投中球的概率为
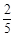，且在各位置投球是否投进互不影响.
（Ⅰ）求该选手被淘汰的概率；
（Ⅱ）该选手在比赛中投球的个数记为ξ，求随机变量ξ的分布列与数学期望Eξ.（注：本小题结果可用分数表示）
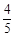，在三分区投中球的概率为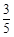，在中场跳球区投中球的概率为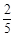，且在各位置投球是否投进互不影响. （Ⅰ）求该选手被淘汰的概率；
（Ⅱ）该选手在比赛中投球的个数记为ξ，求随机变量ξ的分布列与数学期望Eξ.（注：本小题结果可用分数表示）
（Ⅰ）
（Ⅱ）
（Ⅱ）本试题主要是考查了独立事件概率的乘法公式的运用以及随机变量的分布列的求解和数学期望值的综合运用 。
（1）因为记“该选手能投进第
个球”的事件为
，
则
，
，
，
该选手被淘汰的概率
则利用乘法公式可知。
（2）根据题意可知
的可能值为
，
，
，
从而得到分布列和期望值。
解：（Ⅰ）解法一：记“该选手能投进第个球”的事件为，
则，，，
该选手被淘汰的概率
.
（Ⅰ）解法二：记“该选手能投进第个球”的事件为，
则，，.
该选手被淘汰的概率
.
（Ⅱ）的可能值为，，
，
.
的分布列为
.
（1）因为记“该选手能投进第
个球”的事件为，则
，，，该选手被淘汰的概率则利用乘法公式可知。
（2）根据题意可知
的可能值为，，，从而得到分布列和期望值。
解：（Ⅰ）解法一：记“该选手能投进第
个球”的事件为，则
，，，该选手被淘汰的概率.（Ⅰ）解法二：记“该选手能投进第
个球”的事件为，则
，，.该选手被淘汰的概率.（Ⅱ）
的可能值为，，，.的分布列为.
练习册系列答案
相关题目
，乙每次击中目标的概率为
，两人间每次射击是否击中目标互不影响。
，
，
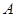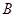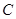三个不同的元件连接成一个系统
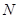.当元件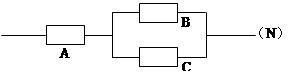
的概率分布如下，则P的值等于 ( )
C. 
，则方差
．
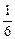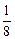
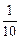
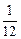
，而且三好学生中女生占一半，现在从该班任选一名学生参加座谈会，则在已知没有选上女生的条件下，选上的是三好学生的概率是（ ）
，现在三人同时射击一个目标，目标被命中的概率是
