题目内容
已知函数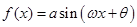 的部分图象如下图,其中
的部分图象如下图,其中
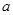 是
是 的角
的角 所对的边.
所对的边.
(1)求 的解析式;
的解析式;
(2)若 中角
中角 所对的边
所对的边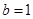 ,
, ,求
,求 的面积
的面积 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据图像可知 的最大值为
的最大值为 ,可知
,可知 ,再根据周期
,再根据周期 可得
可得 ,再由的
,再由的 图像一个最高点的坐标为
图像一个最高点的坐标为 可知
可知 ,从而
,从而 ,结合
,结合 ,可得
,可得 ,因此所求解析式为
,因此所求解析式为 ;(2)根据面积计算公式
;(2)根据面积计算公式 可知只需求得
可知只需求得 的值,即可求得
的值,即可求得 的面积,而条件中
的面积,而条件中 结合(1)中所求,即可建立关于
结合(1)中所求,即可建立关于 的方程,从而求得
的方程,从而求得 的值:由
的值:由 得,
得, ,即
,即 ,联立
,联立 ,得
,得 ,
, .
.
试题解析:(1)∵ ,由图像可知
,由图像可知 , 2分
, 2分
函数 的最小正周期
的最小正周期 ,得
,得  , 3分
, 3分
由 ,得
,得 , 4分
, 4分
∵ ,∴
,∴ , 5分
, 5分
故 ; 6分
; 6分
(2)由 得,
得, , 7分
, 7分
即 , 8分
, 8分
又∵ ,得
,得 , 10分
, 10分
由 得,
得, , 11分
, 11分 . 13分
. 13分
考点:1.三角函数的图像和性质;2.三角恒等变形.

练习册系列答案
相关题目
 的图像关于直线
的图像关于直线 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为 .
. 和
和 的值;
的值; ,求
,求 的值.
的值. ,且
,且 的图象的一个对称中心到最近的对称轴的距离为
的图象的一个对称中心到最近的对称轴的距离为 ,(1)求
,(1)求 的值;(2)求
的值;(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
 的周期和单调递增区间;
的周期和单调递增区间; 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围.
 ;
; ,且
,且 ,求
,求 的值.
的值. 在区间
在区间 上的图像(完成列表并作图)。
上的图像(完成列表并作图)。



 和
和 为方程
为方程 的两根,求
的两根,求 ;(2)
;(2) 的值。
的值。 ,
, .
. 是函数
是函数 的一个零点,求
的一个零点,求 的值;
的值; 的单调递增区间.
的单调递增区间. )+2a+b,当x∈[0,
)+2a+b,当x∈[0, ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1. ,则
,则
 .
.