题目内容
已知等差数列{an}中,a1=1,公差d=2,则数列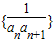 的前n项和为 .
的前n项和为 .
【答案】分析:写出an,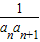 ,利用裂项相消法可求得数列
,利用裂项相消法可求得数列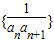 的前n项和.
的前n项和.
解答:解:an=1+(n-1)×2=2n-1,
则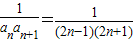 =
= (
(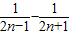 ),
),
所以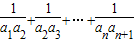
= (1-
(1- )+
)+ (
(
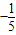 )+
)+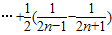
= (1-
(1-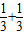
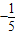 +…+
+…+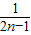
 )
)
= (1-
(1-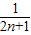 )=
)=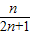 ;
;
故答案为: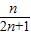 .
.
点评:本题考查等差数列的通项公式、裂项相消法对数列求和,属中档题.
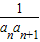 ,利用裂项相消法可求得数列
,利用裂项相消法可求得数列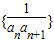 的前n项和.
的前n项和.解答:解:an=1+(n-1)×2=2n-1,
则
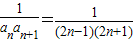 =
= (
(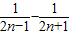 ),
),所以
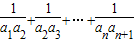
=
 (1-
(1- )+
)+ (
(
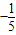 )+
)+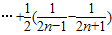
=
 (1-
(1-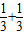
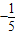 +…+
+…+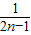
 )
)=
 (1-
(1-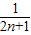 )=
)=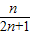 ;
;故答案为:
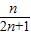 .
.点评:本题考查等差数列的通项公式、裂项相消法对数列求和,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.