题目内容

若函数f（x）在定义域D内某区间I上是增函数，而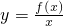 $数学公式$ 在I上是减函数，则称y=f（x）在I上是“弱增函数”．已知f（x）=x²+（cotθ-1）x+b（θ、b是常数，b＞0）．
（1）若f（x）是偶函数，求θ、b应满足的条件；
（2）当cotθ≥1时，f（x）在（0，1]上是“弱增函数”，求实数b的范围．
（3）当cotθ≥1时，f（x）在（0，1]上不是“弱增函数”，求实数b的范围．

解：（1）若f（x）是偶函数，则f（x）=f（-x），
即x²+（cotθ-1）x+b=x²-（cotθ-1）x+b对任意x∈R恒成立，
∴cotθ=1，b＞0，∴若f（x）是偶函数，则 $\text{[math]}$ ，
（2）当cotθ≥1时，f（x）=x²+（cotθ-1）x+b的对称轴是 $\text{[math]}$
∴f（x）在（0，1]上是增函数，
考察函数 $\text{[math]}$ ，
当 $\text{[math]}$ ，即b≥1时，设0＜x₁＜x₂≤1，则 $\text{[math]}$
∵0＜x₁＜x₂≤1，∴x₁-x₂＜0，0＜x₁x₂＜1≤b，
∴ $\text{[math]}$
即g（x）在（0，1]上单调递减，f（x）在（0，1]上是“弱增函数”；
综上所述，b≥1时，f（x）在（0，1]上是“弱增函数”；
（3）当 $\text{[math]}$ ，即0＜b＜1时，g（b）=g（1）=1+b+（cotθ-1），
即g（x）在（0，1]上不是单调函数，
∴f（x）在（0，1]上不是“弱增函数”．
综上所述0＜b＜1时，f（x）在（0，1]上不是“弱增函数”
分析：（1）利用偶函数的定义，可得x²+（cotθ-1）x+b=x²-（cotθ-1）x+b对任意x∈R恒成立，由此可求θ、b应满足的条件；
（2）确定f（x）在（0，1]上是增函数，考察函数 $\text{[math]}$ ，g（x）在（0，1]上单调递减，f（x）在（0，1]上是“弱增函数”，由此可得结论；
（3）结合（2），利用新定义，即可求实数b的范围．
点评：本题考查新定义，考查学生分析解决问题的能力，正确运用新定义是关键．