题目内容
若F是双曲线 的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且
的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且 ,则
,则 = .
= .
【答案】分析:不妨设F是双曲线的左焦点,则F(- ,0),根据
,0),根据 ,用坐标表示向量,再利用双曲线的第二定义求出焦半径,即可得出结论.
,用坐标表示向量,再利用双曲线的第二定义求出焦半径,即可得出结论.
解答:解:不妨设F是双曲线的左焦点,则F(- ,0)
,0)
设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),
∵ ,
,
∴((x1+ ,y1)+((x2+
,y1)+((x2+ ,y2)+((x3+
,y2)+((x3+ ,y3)+(x4+
,y3)+(x4+ ,y4)=(0,0)
,y4)=(0,0)
∴x1+x2+x3+x4=-4
∵ ,
, ,
, ,
,
∴ =-8-
=-8- (x1+x2+x3+x4)=-8-
(x1+x2+x3+x4)=-8- =6
=6
故答案为:6.
点评:本题重点考查双曲线的第二定义,考查向量知识的运用,解题的关键是用坐标表示向量,属于中档题.
 ,0),根据
,0),根据 ,用坐标表示向量,再利用双曲线的第二定义求出焦半径,即可得出结论.
,用坐标表示向量,再利用双曲线的第二定义求出焦半径,即可得出结论.解答:解:不妨设F是双曲线的左焦点,则F(-
 ,0)
,0)设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),
∵
 ,
,∴((x1+
 ,y1)+((x2+
,y1)+((x2+ ,y2)+((x3+
,y2)+((x3+ ,y3)+(x4+
,y3)+(x4+ ,y4)=(0,0)
,y4)=(0,0)∴x1+x2+x3+x4=-4

∵
 ,
, ,
, ,
,
∴
 =-8-
=-8- (x1+x2+x3+x4)=-8-
(x1+x2+x3+x4)=-8- =6
=6故答案为:6.
点评:本题重点考查双曲线的第二定义,考查向量知识的运用,解题的关键是用坐标表示向量,属于中档题.

练习册系列答案
相关题目
 的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且
的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且 ,则
,则 ________
________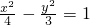 的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且
的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且 ,则
,则 =________.
=________. 的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且
的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且 ,则
,则 = .
= . 的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且
的一个焦点,P1、P2、P3、P4是双曲线上同一支上任意4个不同的点,且 ,则
,则 = .
= .