题目内容
已知数列 满足
满足
(1) 求数列 的通项公式;
的通项公式;
(2) 设b =
= (n∈N
(n∈N ,n≥2), b
,n≥2), b ,求证:b
,求证:b +b
+b +……+b
+……+b < 3 .
< 3 .
 满足
满足
(1) 求数列
 的通项公式;
的通项公式;(2) 设b
 =
= (n∈N
(n∈N ,n≥2), b
,n≥2), b ,求证:b
,求证:b +b
+b +……+b
+……+b < 3 .
< 3 .(1);(2)同解析;
(1)∵ ∴
∴
∴数列{ }是以首项a1+1,公比为2的等比数列,
}是以首项a1+1,公比为2的等比数列,
即

(2)b =
= =
= =
=
 ≤
≤ (n≥2)
(n≥2)
∴b +b
+b +……+b
+……+b =1+
=1+


n=1时,b ="1<3" 成立, 所以b
="1<3" 成立, 所以b +b
+b +……+b
+……+b < 3
< 3
 ∴
∴
∴数列{
 }是以首项a1+1,公比为2的等比数列,
}是以首项a1+1,公比为2的等比数列,即


(2)b
 =
= =
= =
= ≤
≤ (n≥2)
(n≥2)∴b
 +b
+b +……+b
+……+b =1+
=1+


n=1时,b
 ="1<3" 成立, 所以b
="1<3" 成立, 所以b +b
+b +……+b
+……+b < 3
< 3 
练习册系列答案
相关题目
 ,求
,求 及
及 .
.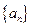 满足
满足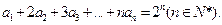
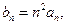 求数列
求数列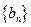 的前
的前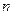 项和
项和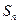 .
.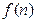 为正整数n(十进制)的各数位上的数字的平方之和,比如
为正整数n(十进制)的各数位上的数字的平方之和,比如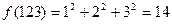 。记
。记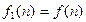 ,
,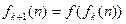 ,
,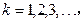 则
则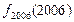 =
= 满足:
满足: ,则
,则 _______.
_______. 中,
中, 时,
时, ,则通项公式
,则通项公式 = 高。资源。网。。。
= 高。资源。网。。。 …,
…, 是各项不为零的
是各项不为零的 项等差数列,且公差
项等差数列,且公差 。若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对
。若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对 所组成的集合为 。
所组成的集合为 。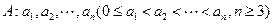 具有性质P:对任意
具有性质P:对任意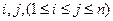 ,
,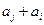 与
与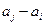 两数中至少有一个是该数列中的一项,现给出以下四
两数中至少有一个是该数列中的一项,现给出以下四 个命题:
个命题: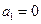 ;
;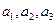
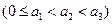 具有性质P,则
具有性质P,则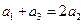 ;
; 中,
中, 是首项为1公比为
是首项为1公比为 的等比数列,则
的等比数列,则 等于 ()
等于 ()


