题目内容
(本小题10分) 等比数列{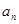 }的前n 项和为
}的前n 项和为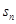 ,已知
,已知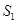 ,
,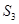 ,
,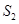 成等差数列
成等差数列
(1)求{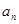 }的公比q;
}的公比q;
(2)求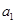 -
-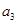 =3,求
=3,求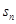 ;
;
【答案】
(1) ;(2)
;(2) 。
。
【解析】
试题分析:(1)依题意有  ,由于
,由于
 ,故
,故  ,故可得公比的值。
,故可得公比的值。
(2)由已知可得 ,从而得到首项的值,并求解和式。
,从而得到首项的值,并求解和式。
(1)依题意有 
由于  ,故
,故 
又 ,从而
,从而 5分
5分
(2)由已知可得
故
从而 10分
10分
考点:本题主要考查等比数列和等差数列的通项公式以及前n项和的关系式的求解运用。
点评:解决该试题的关键是数量的运用等差数列和等比数列的前n项和公式得到基本量的关系式,进而得到结论。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
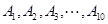 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
.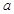 元,该同学决定按
元,该同学决定按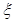 的分布列及数学期望.
的分布列及数学期望. ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求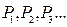 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对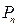 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求