Question

一张1.4 m高的图片挂在墙上，它的底边高于观察者的眼1.8 m，问观察者应站在距墙多远处看图，才能最清晰（即视角最大，视角是指观察图片的上底的视线与观察图片下底的视线所夹的角）?

Answer 1

分析：如图，AB为图片，AB=1.4 m，AO=1.8 m，要求角α的最大值，由已知条件可转化为求tanα的最大值，从而求得距离OD.

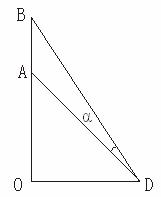
解：设OD=x，∠ADO=β，∠BDO=γ，则α=γ－β，tanγ=，tanβ=，tanα=tan（γ－β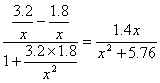）==（x>0）.

令（tanα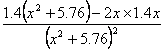）′==0，

解得x=2.4.在x=2.4附近，导数值由正到负，在x=2.4 m处，tanα取得最大值.

答：观察者站在距墙2.4 m处看图最清晰.