题目内容

下面有五个命题：
（1）要得到y=2sin(2x+

2π

)图象，需要将函数y=2sin2x图象向左平移

2π

个单位；
（2）在△ABC中，表达式cos（B+C）+cosA为常数；
（3）设

，

分别是单位向量，则|

|=2；
（4）y=cosx（0≤x≤2π）的图象和直线y=1围成一个封闭的平面图形，该图形的面积是2π．
其中真命题的序号是______（写出所有真命题的编号）

（1）由图象变换的知识可知，要得到y=2sin(2x+

2π

)图象，需要将函数y=2sin2x图象向左平移

个单位，故（1）为假命题．
（2）在△ABC中，表达式cos（B+C）+cosA=cos（π-A）+cosA=-cosA+cosA=0，故为常数，故（2）为真命题．
（3）设

，

分别是单位向量，只有向量

，

同向时，才有|

|=2，故（3）为假命题．
（4）y=cosx（0≤x≤2π）的图象和直线y=1围成一个封闭的平面图形，由定积分的知识可知，该图形的面积S=

∫

2π0

(1-cosx)dx=(x-sinx)

2π0

=(2π-0)-（0-0）=2π．故（4）为真命题．
故答案为（2）（4）

练习册系列答案

学业水平标准与考试说明系列答案

下面有五个命题：
（1）函数y=sin⁴x-cos⁴x的最小正周期是π；
（2）终边在y轴上的角的集合是{a|a= $数学公式$ ，k∈Z}；　
（3）在同一坐标系中，函数y=sinx的图象和y=x的图象仅有一个公共点；
（4）把函数y=3sin（2x+ $数学公式$ ）的图象向右平移 $数学公式$ 个单位得到y=sin2x的图象；
（5）函数y=sin（ $数学公式$ -x）在（0，π）上是增函数．
其中，真命题的编号是________．（写出所有真命题的编号）

下面有五个命题：
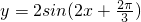（1）要得到 $数学公式$ 图象，需要将函数y=2sin2x图象向左平移 $数学公式$ 个单位；
（2）在△ABC中，表达式cos（B+C）+cosA为常数；
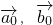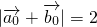（3）设 $数学公式$ 分别是单位向量，则 $数学公式$ ；
（4）y=cosx（0≤x≤2π）的图象和直线y=1围成一个封闭的平面图形，该图形的面积是2π．
其中真命题的序号是________（写出所有真命题的编号）