题目内容
下表给出的是由n×n(n≥3,n∈N*))个正数排成的n行n列数表,aij表示第i行第j列的一个数,表中第一列的数从上到下依次成等差数列,其公差为d,表中各行,每一行的数从左到右依次都成等比数列,且所有公比相等,公比为q,已知 .
.(1)求a11,d,q的值;
(2)设表中对角线上的数a11,a22,a33,…,ann组成的数列为{an},记Tn=a11+a22+a33+…+ann,求使不等式2nTn<4n-n-43成立的最小正整数n.
| a11 | a12 | a13 | … | a1n |
| a21 | a22 | a23 | … | a2n |
| a31 | a32 | a33 | … | a3n |
| … | … | … | … | … |
| an1 | an2 | an3 | … | ann |
【答案】分析:(1)已知 .可得
.可得 ,从而可求a11,d,q的值;
,从而可求a11,d,q的值;
(2)先表示出 ,从而可求和,进而可求使不等式2nTn<4n-n-43成立的最小正整数n.
,从而可求和,进而可求使不等式2nTn<4n-n-43成立的最小正整数n.
解答:解:(1)根据题意,∵aij表示第i行第j列的一个数,表中第一列的数从上到下依次成等差数列,其公差为d,表中各行,每一行的数从左到右依次都成等比数列,且所有公比相等,公比为q,
所以可得得 ,
,
∴
(2)
∵Tn=a11+a22+a33+…+ann,
∴
∴
两式相减整理得:∴
∴4n-3×2n-40>0,∴n>3
故使不等式2nTn<4n-n-43成立的最小正整数n为4.
点评:本题以数列为载体,考查新定义,考查解方程组,考查错位相减法求和,有一定的综合性.
 .可得
.可得 ,从而可求a11,d,q的值;
,从而可求a11,d,q的值;(2)先表示出
 ,从而可求和,进而可求使不等式2nTn<4n-n-43成立的最小正整数n.
,从而可求和,进而可求使不等式2nTn<4n-n-43成立的最小正整数n.解答:解:(1)根据题意,∵aij表示第i行第j列的一个数,表中第一列的数从上到下依次成等差数列,其公差为d,表中各行,每一行的数从左到右依次都成等比数列,且所有公比相等,公比为q,
所以可得得
 ,
,∴

(2)

∵Tn=a11+a22+a33+…+ann,
∴

∴

两式相减整理得:∴

∴4n-3×2n-40>0,∴n>3
故使不等式2nTn<4n-n-43成立的最小正整数n为4.
点评:本题以数列为载体,考查新定义,考查解方程组,考查错位相减法求和,有一定的综合性.

练习册系列答案
相关题目
(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表, 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为 ,若已知
,若已知
 |  |  | … |  |
 |  |  | … |  |
 |  |  | … |  |
| … | … | … | … | … |
 |  |  | … |  |
 的值;
的值;(2)求用
 表示
表示 的代数式;
的代数式;(3)设表中对角线上的数
 ,
, ,
, ,……,
,……, 组成一列数列,设Tn=
组成一列数列,设Tn= +
+ +
+ +……+
+……+ 求使不等式
求使不等式 成立的最小正整数n.
成立的最小正整数n. (本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表, 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为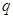 ,若已知
,若已知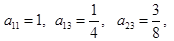
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
|
|
|
|
… |
|
(1)求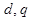 的值;
的值;
(2)求用 表示
表示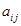 的代数式;
的代数式;
(3)设表中对角线上的数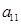 ,
,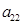 ,
,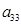 ,……,
,……, 组成一列数列,设Tn=
组成一列数列,设Tn=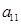 +
+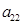 +
+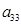 +……+
+……+ 求使不等式
求使不等式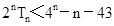 成立的最小正整数n.
成立的最小正整数n.











