题目内容
等比数列的前n项的和Sn=k•3n+1,则k的值为______.
(法一)n=1时,a1=S1=3k+1
当n≥2时,an=Sn-Sn-1=k•3n+1-k•3n-1-1=2k•3n-1
数列为等比数列可知a1=3k+1适合上式,则2k=3k+1
∴k=-1
(法二)由等比数列的前n项和公式可得Sn=
=
-
•qn
∵Sn=1+k•3n
∴
=1,k=-
=-1
故答案为:-1
当n≥2时,an=Sn-Sn-1=k•3n+1-k•3n-1-1=2k•3n-1
数列为等比数列可知a1=3k+1适合上式,则2k=3k+1
∴k=-1
(法二)由等比数列的前n项和公式可得Sn=
| a1(1-qn) |
| 1-q |
| a1 |
| 1-q |
| a1 |
| 1-q |
∵Sn=1+k•3n
∴
| a1 |
| 1-q |
| a1 |
| 1-q |
故答案为:-1

练习册系列答案
相关题目
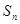 为等比数列
为等比数列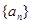 的前n项的和,
的前n项的和,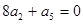 ,则
,则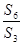 =___________
=___________ 为等比数列
为等比数列 的前n项的和,
的前n项的和, ,则
,则 =
=