题目内容
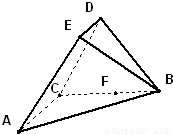
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱EF
BC.
(1)证明FO∥平面CDE;
(2)设BC=
CD,证明EO⊥平面CDF.
证明:(1)取CD中点M,连结OM,在矩形ABCD中,
OM
BC,又EF
BC,则EF
OM.连结EM,
于是四边形EFOM为平行四边形.
∴FO∥EM.
又∵FO
平面CDE,且EM
平面CDE,
∴FO∥平面CDE.
(2)连结FM.由(1)和已知条件,在等边△CDE中,
CM=DM,EM⊥CD且EM=
CD=
BC=EF.
因此平行四边形EFOM为菱形,从而EO⊥FM.
∵CD⊥OM,CD⊥EM,
∴CD⊥平面EOM.从而CD⊥EO.
而FM∩CD=M,所以EO⊥平面CDF.
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
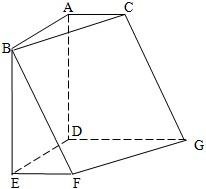如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG．且AB=AD=DE=DG=2，AC=EF=1．
如图，在五面体ABCDE中，平面BCD⊥平面ABC，DC=DB=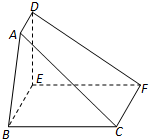
如图，在五面体ABC-DEF中，四边形BCFE 是矩形，DE⊥平面BCFE．
，AC=BC=2ED=2，AC⊥BC，且ED∥AC 
，求二面角F-AE-B的余弦值．
