题目内容
已知抛物线y=x2-4与直线y=x+2,求:(1)它们的交点;
(2)抛物线在交点处的切线方程.
解:(1)联立两方程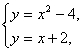
得两交点为A(-2,0),B(3,5).
(2)因为y'=![]()
![]() =
=![]()
![]() =2x,
=2x,
所以y'|x=-2=-4, y'|x=3=6.
所以两切线方程分别为
y=-4(x+2),y-5=6(x-3),
即4x+y+8=0,6x-y-13=0.

练习册系列答案
相关题目
已知抛物线y=-x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于( )
| A、3 | ||
| B、4 | ||
C、3
| ||
D、4
|
已知抛物线y=x2上有一定点A(-1,1)和两动点P、Q,当PA⊥PQ时,点Q的横坐标取值范围是( )
| A、(-∞,-3] | B、[1,+∞) | C、[-3,1] | D、(-∞,-3]∪[1,+∞) |