题目内容
已知函数f(x)=(| 1 |
| 2 |
(1)判断并证明f(x)的奇偶性;
(2)作f(x)的图象,并根据图象指出其单调区间;
(3)若函数g(x)=(
| 1 |
| 2 |
分析:(1)利用奇偶函数的定义判断即可;
(2)作出函数y= (
)x (x≥0)的图象,就是f(x)=(
)|x|y轴右侧的图象,然后利用偶函数的图象的对称性作出f(x)=(
)|x|左侧的图象即可得到f(x)的图象,再根据图象可得其单调区间;
(3)利用g(x)与f(x)的函数关系式之间的关系利用图象的变换可解决问题.
(2)作出函数y= (
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)利用g(x)与f(x)的函数关系式之间的关系利用图象的变换可解决问题.
解答:解:(1)∵函数f(x)=(
)|x|的定义域为R
∴定义域关于原点对称
又∵f(-(
)|-x| =(
)|x|=f(x)
∴f(x)为偶函数
(2)由于f(x)为偶函数故只需作出函数y= (
)x (x≥0)的图象,就是f(x)=(
)|x|y轴右侧的图象再将图象关于y轴对称即可得到f(x)的图象(如右图).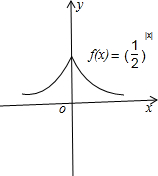
由图可知f(x)的增区间为(-∞,0),减区间为[0.+∞)
(3)∵f(x)=(
)|x|
∴f(x-2)=(
)|x-2|=g(x)
∴将f(x)的图象向右平移2个单位即得g(x)的图象
又由f(x)的图象可知函数f(x)的值域为(0,1]而g(x)的图象可将f(x)的图象向右平移2个单位得到故g(x)的值域为(0,1].
| 1 |
| 2 |
∴定义域关于原点对称
又∵f(-(
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)为偶函数
(2)由于f(x)为偶函数故只需作出函数y= (
| 1 |
| 2 |
| 1 |
| 2 |

由图可知f(x)的增区间为(-∞,0),减区间为[0.+∞)
(3)∵f(x)=(
| 1 |
| 2 |
∴f(x-2)=(
| 1 |
| 2 |
∴将f(x)的图象向右平移2个单位即得g(x)的图象
又由f(x)的图象可知函数f(x)的值域为(0,1]而g(x)的图象可将f(x)的图象向右平移2个单位得到故g(x)的值域为(0,1].
点评:本题考查利用函数的性质(奇偶性)作函数f(x)的图象,然后再利用图象的变换作g(x)的图象进而求函数的单调区间和值域.解决的捷径是数形结合,是中档题.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|