题目内容
在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小;
)的大小;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ∥平面
∥平面![]() ?若
?若![]() 存在,求
存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

(Ⅰ)证明:因为 ![]() ,
,
所以 ![]() . …
. …![]() …………………………………1分
…………………………………1分
因为 平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以 ![]() 平面
平面![]() . ………………………………………3分
. ………………………………………3分
![]() (Ⅱ)解:取
(Ⅱ)解:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() ,
,
所以 ![]() .
.
因为 平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以 ![]() 平面
平面![]() . ………………………………………4分
. ………………………………………4分
如图,

以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,在平面
轴,在平面![]() 内过
内过![]() 垂直于
垂直于![]() 的直
的直
线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .不妨设
.不妨设![]() .由
.由
直角梯形![]() 中
中![]() 可得
可得![]() ,
,![]() ,
,
![]() .
.
所以 ![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() .
.
因为 
所以 
即
令![]() ,则
,则![]() .
.
所以 ![]() . ………………………………………7分
. ………………………………………7分
取平面![]() 的一个法向量n
的一个法向量n![]() .
.
所以  .
.
所以 平面![]() 和平面
和平面![]() 所成的二面角(小于
所成的二面角(小于![]() )的大小为
)的大小为![]() .
.
![]() ………………………………………9分
………………………………………9分
(Ⅲ)解:在棱![]() 上存在点
上存在点![]() 使得
使得![]() ∥平面
∥平面![]() ,此时
,此时![]() . 理由如
. 理由如
下: ![]() ………………………………………10分
………………………………………10分

取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 则
则 ![]() ∥
∥![]() ,
,![]() .
.
因为 ![]() ,
,
所以 ![]() .
.
因为 ![]() ∥
∥![]() ,
,
所以 四边形![]() 是平行四边形.
是平行四边形.
所以 ![]() ∥
∥![]() .
.
因为 ![]() ,
,
所以 平面![]() ∥平面
∥平面![]() . ………………………………………13分
. ………………………………………13分
因为 ![]() 平面
平面![]() ,
,
所以 ![]() ∥平面
∥平面![]() . ………………………………………14分
. ………………………………………14分

练习册系列答案
相关题目
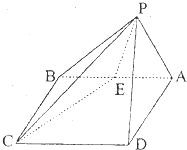 如图在四棱锥P-ABCD中,侧面PAD是边长为a的正三角形,二面角P-AD-B为直二面角,ABCD是矩形,E是AB中点,PC与底面ABCD成30°角.
如图在四棱锥P-ABCD中,侧面PAD是边长为a的正三角形,二面角P-AD-B为直二面角,ABCD是矩形,E是AB中点,PC与底面ABCD成30°角. 在直四棱柱ABCD-A1B1C1D1中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,C1O与平面ABCD所成的角为60°.
在直四棱柱ABCD-A1B1C1D1中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,C1O与平面ABCD所成的角为60°.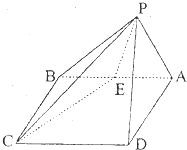 如图在四棱锥P-ABCD中,侧面PAD是边长为a的正三角形,二面角P-AD-B为直二面角,ABCD是矩形,E是AB中点,PC与底面ABCD成30°角.
如图在四棱锥P-ABCD中,侧面PAD是边长为a的正三角形,二面角P-AD-B为直二面角,ABCD是矩形,E是AB中点,PC与底面ABCD成30°角.
 角.
角.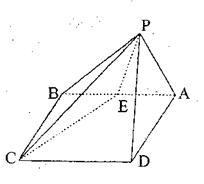 (I)求二面角P—EC—D的大小;
(I)求二面角P—EC—D的大小;