Question

已知等比数列{a_n}满足a₁+a₆=11,且a₃a₄=.

(1)求数列{a_n}的通项公式；

（2）如果至少存在一个自然数m，恰使a_m-1,a_m²,a_m+1+这三个数依次成等差数列，问这样的等比数列{a_n}是否存在，若存在，求出通项公式；若不存在，说明理由.

Answer 1

解：（1）∵a₁a₆=a₃a₄=，且a₁a₆=11,

∴以a₁,a₆为根的一元二次方程为x²-11x+=0.

解之得

∴

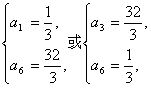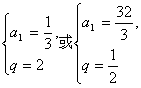
∴数列{a_n}的通项公式为

a_n=×2^n-1或a_n=×()^n-1=×2^6-n,n∈N₊.

(2)对a_n=×2^n-1,若存在题设要求的m，则

2(×2^m-1)²=××2^m-2+×2^m+,

∴(2^m)²-7×2^m-8=0,

∴2^m=8,m=3.

若对a_n=×2^6-n存在题设要求的m，同理有

4(2^6-m)²-11×2^6-m-8=0.

而Δ=11²+16×8不是完全平方数.

故此时所需的m不存在.

综上，满足条件的等比数列存在，且有a_n=.