题目内容
(本小题满分12分)如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是 的中点.
的中点.
(1)求证: ;
;
(2)若直线 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.

【答案】
(I)证明:见解析;(Ⅱ)异面直线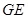 与
与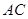 所成角的余弦值为
所成角的余弦值为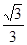 .
.
【解析】本题主要考查线线垂直,线面垂直,面面垂直间的转化以及异面直线所成的角的求法
(I)由矩形ADEF可知ED⊥AD,又因为平面ADEF⊥平面ABCD,得到ED⊥平面ABCD,从而有ED⊥AC.(Ⅱ)由(I)ED⊥平面ABCD,可知∠EDB是直线BE与平面ABCD所成的角,又由AM∥GE,知∠MAC是异面直线GE与AC所成角或其补角然后在△MAC中用余弦定理求解.
(I)证明:在矩形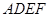 中,
中,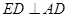
∵ 平面
 平面
平面 ,且平面
,且平面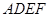
 平面
平面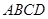
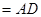
∴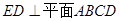 ∴
∴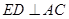 --------------6分
--------------6分
(Ⅱ)由(I)知: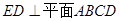
∴ 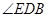 是直线
是直线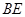 与平面
与平面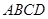 所成的角,即
所成的角,即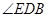
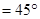 -----------8分
-----------8分
设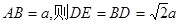 ,取
,取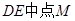 ,连接
,连接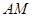 ∵
∵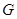 是
是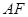 的中点
的中点
∴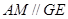 ∴
∴ 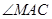 是异面直线
是异面直线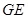 与
与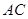 所成角或其补角--------10分
所成角或其补角--------10分
连接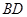 交
交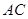 于点
于点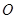 ∵
∵ 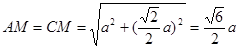 ,
,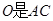 的中点
的中点
∴ 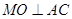 ∴
∴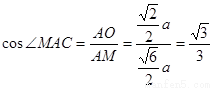
∴ 异面直线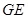 与
与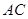 所成角的余弦值为
所成角的余弦值为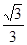 .-------12分
.-------12分

练习册系列答案
相关题目