题目内容
已知函数f(x)=cos2x+2sinxcosx-sin2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间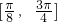 上的最大值和最小值及取得最大最小值时对应x的值.
上的最大值和最小值及取得最大最小值时对应x的值.
解:(1)函数f(x)=cos2x+2sinxcosx-sin2x=cos2x+sin2x= sin(2x+
sin(2x+ ),故函数的最小正周期等于
),故函数的最小正周期等于 =π.
=π.
(2)∵ ≤x≤
≤x≤ ,∴
,∴ ≤2x+
≤2x+ ≤
≤ ,∴-1≤sin(2x+
,∴-1≤sin(2x+ )≤1,∴-
)≤1,∴- ≤f(x)≤
≤f(x)≤ .
.
当2x+ =
= ,即x=
,即x= 时,函数f(x)取得最小值为-
时,函数f(x)取得最小值为- ,当2x+
,当2x+ =
= ,即x=
,即x= 时,函数f(x)取得最大值为
时,函数f(x)取得最大值为  .
.
分析:(1)利用两角和差的正弦公式、二倍角公式化简函数f(x)的解析式为 sin(2x+
sin(2x+ ),由此求得函数的最小正周期.
),由此求得函数的最小正周期.
(2)根据x的范围求得2x+ 的范围,从而求得sin(2x+
的范围,从而求得sin(2x+ )的范围,可得函数f(x)的最值,以及取得最大最小值时对应x的值.
)的范围,可得函数f(x)的最值,以及取得最大最小值时对应x的值.
点评:本题主要考查两角和差的正弦公式、二倍角公式,正弦函数的周期性、定义域和值域,属于中档题.
 sin(2x+
sin(2x+ ),故函数的最小正周期等于
),故函数的最小正周期等于 =π.
=π.(2)∵
 ≤x≤
≤x≤ ,∴
,∴ ≤2x+
≤2x+ ≤
≤ ,∴-1≤sin(2x+
,∴-1≤sin(2x+ )≤1,∴-
)≤1,∴- ≤f(x)≤
≤f(x)≤ .
.当2x+
 =
= ,即x=
,即x= 时,函数f(x)取得最小值为-
时,函数f(x)取得最小值为- ,当2x+
,当2x+ =
= ,即x=
,即x= 时,函数f(x)取得最大值为
时,函数f(x)取得最大值为  .
.分析:(1)利用两角和差的正弦公式、二倍角公式化简函数f(x)的解析式为
 sin(2x+
sin(2x+ ),由此求得函数的最小正周期.
),由此求得函数的最小正周期.(2)根据x的范围求得2x+
 的范围,从而求得sin(2x+
的范围,从而求得sin(2x+ )的范围,可得函数f(x)的最值,以及取得最大最小值时对应x的值.
)的范围,可得函数f(x)的最值,以及取得最大最小值时对应x的值.点评:本题主要考查两角和差的正弦公式、二倍角公式,正弦函数的周期性、定义域和值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )