题目内容
已知函数f(x)是奇函数,其定义域为(-1,1),且在[0,1)上是增函数,若f(a-2)+f(3-2a)<0,试求a的取值范围.
解:函数f(x)是奇函数,且在[0,1)上是增函数,
则f(x)在(-1,0]也是增函数,即f(x)在(-1,1)是增函数,
f(a-2)+f(3-2a)<0?f(a-2)<-f(3-2a)?f(a-2)<f(2a-3),
又由f(x)在(-1,1)是增函数,
则有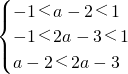 ,解可得1<a<2,
,解可得1<a<2,
故a的取值范围是1<a<2.
分析:根据题意,由奇函数在对称区间单调性相同,可得f(x)在(-1,0]也是增函数,综合可得f(x)在(-1,1)是增函数,进而可以将f(a-2)+f(3-2a)<0变形为f(a-2)<f(2a-3),综合考虑函数的定义域与单调性,可得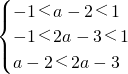 ,解可得答案.
,解可得答案.
点评:本题综合考查函数的奇偶性与单调性,注意奇函数在对称区间单调性相同,并且不能遗忘函数的定义域.
则f(x)在(-1,0]也是增函数,即f(x)在(-1,1)是增函数,
f(a-2)+f(3-2a)<0?f(a-2)<-f(3-2a)?f(a-2)<f(2a-3),
又由f(x)在(-1,1)是增函数,
则有
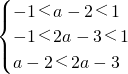 ,解可得1<a<2,
,解可得1<a<2,故a的取值范围是1<a<2.
分析:根据题意,由奇函数在对称区间单调性相同,可得f(x)在(-1,0]也是增函数,综合可得f(x)在(-1,1)是增函数,进而可以将f(a-2)+f(3-2a)<0变形为f(a-2)<f(2a-3),综合考虑函数的定义域与单调性,可得
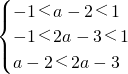 ,解可得答案.
,解可得答案.点评:本题综合考查函数的奇偶性与单调性,注意奇函数在对称区间单调性相同,并且不能遗忘函数的定义域.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目