题目内容
定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,
,
都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
已知函数![]() ;
; ![]()
(1)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的取值范围.
的取值范围.
解:(I)由题意知,![]() 在
在![]() 上恒成立.
上恒成立. ![]() ,
, ![]() ∴
∴![]() 在
在![]() 上恒成立 ∴
上恒成立 ∴  ………………2分
………………2分
设![]() ,
,![]() ,
,![]() ,
,
由![]()
![]() 得 t≥1, 设
得 t≥1, 设![]() ,
,![]()
![]()
![]()
所以![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增, (单调性不证,不扣分))
上递增, (单调性不证,不扣分))
![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
, ![]() 在
在![]() 上的最小值为
上的最小值为![]()
所以实数![]() 的取值范围为
的取值范围为![]() …………………………………………………6分
…………………………………………………6分
(Ⅱ)![]() , ∵ m>0 ,
, ∵ m>0 ,![]() ∴
∴ ![]() 在
在![]() 上递减,
上递减,
∴ ![]() 即
即![]()
∵ ![]() ,
,![]() ∴
∴ ![]() 在
在![]() 上递增,
上递增,
∴ ![]() 即
即![]() …………………………8分
…………………………8分
①当![]() 时,
时,![]() ,
,![]() 此时
此时 ![]()
②当![]() ,即,
,即,![]() ,
,![]() 此时
此时 ![]() ,
,
③当![]() 时,
时,![]() ,此时
,此时 ![]() ……………………11分
……………………11分
综上所述:当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;
;
当![]() 时,
时,![]() 的取值范围是
的取值范围是 ![]() ……………………………12分
……………………………12分

练习册系列答案
相关题目
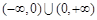 上的函数
上的函数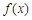 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列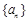 ,
,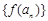 仍是等比数列,则称
仍是等比数列,则称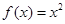 ; ②
; ②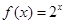 ; ③
; ③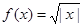 ; ④
; ④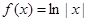 .
.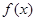 的序号为
的序号为