题目内容
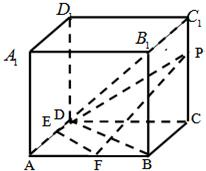已知正方体ABCD-A1B1C1D1中，AB=4，E为AB中点，F为AD中点．P在棱CC1上，C1P=1．（1）求证：AC1∥平面PEF；
（2）求四棱锥P-EFBD的体积．
分析：（1）连AC交EF于G，连PG，根据比例关系可知PG∥AC1，而PG?平面PEF，AC1?平面PEF，根据线面平行的判定定理可知AC1∥平面PEF；
（2）先求出S梯形EFDB=S△ABD-S△AEF，然后求出四棱锥P-EFDB的高PC，最后根据体积公式求出所求即可．
（2）先求出S梯形EFDB=S△ABD-S△AEF，然后求出四棱锥P-EFDB的高PC，最后根据体积公式求出所求即可．
解答：解：（1）连AC交EF于G，连PG（2分）
∵
=
=
∴PG∥AC1（5分）
又∵
，∴AC1∥平面PEF（7分）
（2）∵S梯形EFDB=S△ABD-S△AEF=6（10分）
PC是四棱锥P-EFDB的高∴h=PC=3（12分）
VP-EFDB=
.6.3=6（14分）
∵
| AG |
| AC |
| C1P |
| CC1 |
| 1 |
| 4 |
∴PG∥AC1（5分）
又∵
|
（2）∵S梯形EFDB=S△ABD-S△AEF=6（10分）
PC是四棱锥P-EFDB的高∴h=PC=3（12分）
VP-EFDB=
| 1 |
| 3 |
点评：本题主要考查了直线与平面平行的判定，以及三棱锥的体积的计算，体积的求解在最近两年高考中频繁出现，值得重视．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知正方体ABCD-A1B1C1D1的棱长为2，点P在平面DD1C1C内，PD1=PC1=
已知正方体ABCD-A1B1C1D1，O是底ABCD对角线的交点．