题目内容
设函数f（x），g（x）的定义域分别为M，N，且M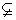
N，若对任意的x∈M，都有g（x）=f（x），则称g（x）是f（x）的“拓展函数”，已知函数
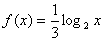，若g（x）是f（x）的“拓展函数”，且g（x）是偶函数，则符合条件的一个g（x）是（ ）。
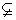N，若对任意的x∈M，都有g（x）=f（x），则称g（x）是f（x）的“拓展函数”，已知函数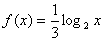，若g（x）是f（x）的“拓展函数”，且g（x）是偶函数，则符合条件的一个g（x）是（ ）。
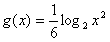（答案不唯一）
练习册系列答案
相关题目