题目内容
如图，⊙O是直角ABC的内切圆，∠ACB=90°且AB=13AC=12，则：该内切圆的半径大小为2
2
；图中阴影部分的面积为30-4π
30-4π
．分析：①利用三角形的面积和切线的性质即可求出；
②利用三角形ABC的面积减去其内切圆的面积即可．
②利用三角形ABC的面积减去其内切圆的面积即可．
解答：解：①如图所示，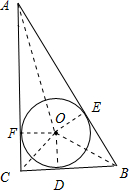
设三个切点分别为D、E、F，连接OA、OB、OC、OD、OE、OF．
则OD⊥BC，OE⊥AB，OF⊥AC．
设内切圆O的半径为r，三条边BC、AC、AB分别为a、b、c，则b=
=5．
则S△OAB+S△OAC+S△OBC=S△ABC，
∴
r(a+b+c)=
ab，
∴r=
=
=2；
②图中阴影部分的面积S=S△ABC-S圆O=
×12×5-π×22=30-4π．
故答案为2，30-4π．
设三个切点分别为D、E、F，连接OA、OB、OC、OD、OE、OF．
则OD⊥BC，OE⊥AB，OF⊥AC．
设内切圆O的半径为r，三条边BC、AC、AB分别为a、b、c，则b=
| c2-a2 |
则S△OAB+S△OAC+S△OBC=S△ABC，
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| ab |
| a+b+c |
| 12×5 |
| 5+12+13 |
②图中阴影部分的面积S=S△ABC-S圆O=
| 1 |
| 2 |
故答案为2，30-4π．
点评：熟练正确三角形的面积公式和其内切圆的性质是解题的关键．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
（1）如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C．求证：BT平分∠OBA
本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，
（几何证明选做题）如图，∠PAQ是直角，半径为5的圆O与AP相切于点T，与AQ相交于两点B、C，BT是否平分∠OBA？证明你的结论；