题目内容
(1)求与椭圆(2)已知双曲线的焦点在y轴上,并且双曲线上两点P1、P2的坐标分别为(3,-4![]() )、(
)、(![]() ,5),求双曲线的标准方程.
,5),求双曲线的标准方程.
分析:
第(1)题由椭圆的方程确定焦点坐标,可求得c值,设双曲线方程为![]() (a>0,b>0),用待定系数法,求得a、b;第(2)题可先设出标准方程,然后把P1、P2点坐标代入方程,联立方程组,求a2、b2的值.
(a>0,b>0),用待定系数法,求得a、b;第(2)题可先设出标准方程,然后把P1、P2点坐标代入方程,联立方程组,求a2、b2的值.
解:(1)椭圆![]() 的焦点为(2
的焦点为(2![]() ,0),(-2
,0),(-2![]() ,0),
,0),
设双曲线的方程为![]() ,则a2+b2=20.
,则a2+b2=20.
又∵过点(3![]() ,
,![]() ),
),
∴![]()
综上,得a2=20-2![]() ,b2=2
,b2=2![]() ,
,
∴双曲线方程为![]()
(2)∵双曲线的焦点在y轴上,
∴设双曲线的标准方程为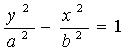 (a>0,b>0), ①
(a>0,b>0), ①
∵点P1、P2在双曲线上,
∴点P1、P2的坐标适合方程①.
将(3,-4![]() ),(
),(![]() ,5)分别代入方程①中,得方程组
,5)分别代入方程①中,得方程组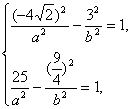
将![]() 看作整体,解得
看作整体,解得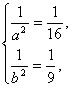
∴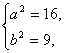 即双曲线的标准方程为
即双曲线的标准方程为![]()
绿色通道:本题只要解得a2、b2即可得到双曲线的方程,不必求出a、b的值;在求解的过程中也可以用换元思想.

练习册系列答案
相关题目
 共焦点的抛物线的标准方程.
共焦点的抛物线的标准方程.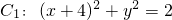 ,
,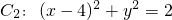 ,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.
,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.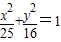 共焦点的抛物线的标准方程.
共焦点的抛物线的标准方程.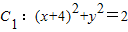 ,
,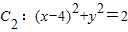 ,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.
,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.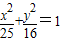 共焦点的抛物线的标准方程.
共焦点的抛物线的标准方程.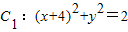 ,
,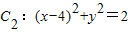 ,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.
,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.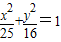 共焦点的抛物线的标准方程.
共焦点的抛物线的标准方程.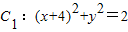 ,
,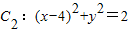 ,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.
,动圆M与两圆一个内切,一个外切,求动圆圆心M的轨迹方程.