题目内容
已知三点O(0,0)、A(3,1)、B(-1,3).若点C满足![]() =α
=α![]() +β
+β![]() ,其中α+β=1,求点C的轨迹方程.
,其中α+β=1,求点C的轨迹方程.
答案:
解析:
提示:
解析:
|
解:设C点坐标为(x,y),∴ 又∵O(0,0)、A(3,1)、B(-1,3), ∴ 又∵ ∴(x,y)=(3α,α)+(-β,3β), 又∵α+β=1,∴ ∴3x+y+3y-x=10,∴2x+4y=10. ∴x+2y=5. ∴点C的轨迹方程为x+2y-5=0. 分析:利用向量的相等构造方程组,解出α、β,再利用α+β=1,去求点C的轨迹方程. |
提示:
|
构造方程组、消去参数α、β是数学中常用的解题思想方法. |

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

 +
+ +
+ 与
与 垂直时C点坐标是(___,____).
垂直时C点坐标是(___,____). +
+ |=
|= ·(
·(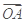 +
+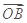 )+2.
)+2.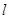 ,点P的坐标是(0,-1),
,点P的坐标是(0,-1),