题目内容
【题目】已知函数
，且曲线
在
处的切线与
平行.
（1）求
的值；
（2）当
时，试探究函数
的零点个数，并说明理由.
【答案】（1）
（2）见解析
【解析】试题分析: （1）根据曲线
在
处的切线与
平行可得: 
,进而求出a值; （2）①当
时， 
，函数
在
单调递增，根据零点存在性定理可得: 
在
上只有一个零点.②当
时， 
恒成立，构造函数
，求导判断单调性与最值可得
，
又
时， 
，所以
，即
，故函数
在
上没有零点，③当
时， 
，
所以函数
在
上单调递减，根据零点存在性定理可得:函数
在
上有且只有一个零点，综上所述
时，函数
有两个零点.
试题解析:解：（1）依题意
，故
，
故
，解得
.
（2）①当
时， 
，此时
， 
，
函数
在
单调递增，
故函数
在
至多有一个零点，又
，
而且函数
在
上是连续不断的，因此函数
在
上只有一个零点.
②当
时， 
恒成立，证明如下：
设
，则
，所以
在
上单调递增，
所以
时， 
，所以
，
又
时， 
，所以
，即
，
故函数
在
上没有零点，
③当
时， 
，
所以函数
在
上单调递减，故函数
在
至多有一个零点，
又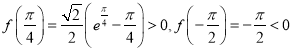
，而且函数
在
上是连续不断的，
因此，函数
在
上有且只有一个零点，
综上所述
时，函数
有两个零点.
名校课堂系列答案
【题目】有甲乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如表的列联表．
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 
（1）请完成如表的列联表；
（2）根据列联表的数据，有多大的把握认为“成绩与班级有关系“？
（3）按分层抽样的方法，从优秀学生中抽出6名学生组成一个样本，再从样本中抽出2名学生，记甲班被抽到的人数为ξ，求ξ的分布列和数学期望．
参考公式和数据：K2= 
，其中n=a+b+c+d
下面的临界值表供参考：
p（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
