题目内容
已知复数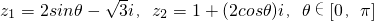 .
.
(1)若z1•z2∈R,求角θ;
(2)复数z1,z2对应的向量分别是 ,
, ,存在θ使等式(λ
,存在θ使等式(λ +
+ )•(
)•( +λ
+λ )=0成立,求实数λ的取值范围.
)=0成立,求实数λ的取值范围.
解:(1)∵z1•z2= =
=
 是实数,
是实数,
∴ ,∴
,∴ ,
,
∵0≤θ≤π,∴0≤2θ≤2π,∴ 或
或 ,解得
,解得 或
或 .
.
(2)∵ =
= +1+(2cosθ)2=8,
+1+(2cosθ)2=8,
 =
= =
= ,
,
∴ =
= +
+
=8λ+ =0,
=0,
化为 ,
,
∵θ∈[0,π],∴
 ,∴
,∴
 .
.
∴ ,解得
,解得 或
或 .
.
实数λ的取值范围是 .
.
分析:(1)根据z1•z2∈R?虚部=0即可求出;
(2)利用复数的几何意义即可得到λ与θ的关系式,进而即可求出λ的取值范围.
点评:熟练掌握z1•z2∈R?虚部=0、复数的几何意义、向量的数量积、一元二次不等式的解法是解题的关键.
 =
=
 是实数,
是实数,∴
 ,∴
,∴ ,
,∵0≤θ≤π,∴0≤2θ≤2π,∴
 或
或 ,解得
,解得 或
或 .
.(2)∵
 =
= +1+(2cosθ)2=8,
+1+(2cosθ)2=8, =
= =
= ,
,∴
 =
= +
+
=8λ+
 =0,
=0,化为
 ,
,∵θ∈[0,π],∴

 ,∴
,∴
 .
.∴
 ,解得
,解得 或
或 .
.实数λ的取值范围是
 .
.分析:(1)根据z1•z2∈R?虚部=0即可求出;
(2)利用复数的几何意义即可得到λ与θ的关系式,进而即可求出λ的取值范围.
点评:熟练掌握z1•z2∈R?虚部=0、复数的几何意义、向量的数量积、一元二次不等式的解法是解题的关键.

练习册系列答案
相关题目
 .
. 最小,并求
最小,并求 .
. (
( 是z的共轭复数),求m和n的值.
是z的共轭复数),求m和n的值.