题目内容
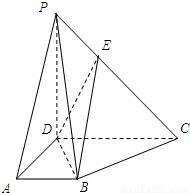
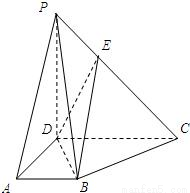
如图，PD⊥平面ABCD，ABCD是边长为2的正方形，PD=1．求异面直线PA与BD所成角的大小．
分析：如图，延长DA至E，CB至F，使得DA=AE，CB=BF连接AF，PF，EF，DF可证得∠PAF（或其补角）的大小即为异面直线PA与BD所成角的大小，在这个三角形中求角即可
解答：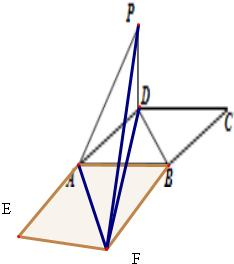
解：如图，延长DA至E，CB至F，使得DA=AE，CB=BF．
连接AF，PF，EF，DF．
因为ABCD是正方形，
所以AD∥BF，且AD=BF，
所以AF∥BD．
故∠PAF（或其补角）的大小即为异面直线PA与BD所成角的大小．
又正方形边长为2，PD=1，
故PA=
，AF=2
，DF=
=2
．
所以，PF=
=
．
于是，cos∠PAF=
=
=-
，
所以异面直线PA与BD所成角的大小为arccos
．
解：如图，延长DA至E，CB至F，使得DA=AE，CB=BF．连接AF，PF，EF，DF．
因为ABCD是正方形，
所以AD∥BF，且AD=BF，
所以AF∥BD．
故∠PAF（或其补角）的大小即为异面直线PA与BD所成角的大小．
又正方形边长为2，PD=1，
故PA=
| 5 |
| 2 |
| CF2+CD2 |
| 5 |
所以，PF=
| PD2+DF2 |
| 21 |
于是，cos∠PAF=
| PA2+AF2-PF2 |
| 2PA•AF |
| 5+8-21 | ||||
2•
|
| ||
| 5 |
所以异面直线PA与BD所成角的大小为arccos
| ||
| 5 |
点评：本题考查异面直线所成的角，其步骤是作角，证角，求角，本题中采用了补形的方法作出了两异面直线所成的角（或其补角）这是求异面直线时常采用的一个技巧．
练习册系列答案
小学课时特训系列答案
相关题目
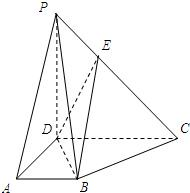如图：PD⊥平面ABCD，四边形ABCD为直角梯形，AB∥CD，∠ADC=90°，PD=CD=2AD=2AB=2，EC=2PE．
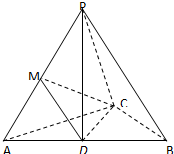如图，PD⊥平面ABC，AC=BC，D，M分别为AB，PA的中点．求证：
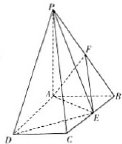如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=1，PD与平面ABCD所成角是30°，点F中PB的中点，点E在边BC上移动．
