题目内容
函数y=x•|1-x|在区间A上是减函数,则A区间是
- A.(-∞,0)
- B.
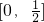
- C.

- D.(
 ,+∞)
,+∞)
C
分析:先分类讨论去掉绝对值,再结合二次函数的图象求出函数y=x•|1-x|的单调递减区间即可.
解答:y=x|1-x|=

再结合二次函数图象可知
函数y=x|1-x|的单调递减区间是( ,1).
,1).
故选C.
点评:本题主要考查了函数的单调性及单调区间,单调性是函数的重要性质,属于基础题.
分析:先分类讨论去掉绝对值,再结合二次函数的图象求出函数y=x•|1-x|的单调递减区间即可.
解答:y=x|1-x|=


再结合二次函数图象可知
函数y=x|1-x|的单调递减区间是(
 ,1).
,1).故选C.
点评:本题主要考查了函数的单调性及单调区间,单调性是函数的重要性质,属于基础题.

练习册系列答案
相关题目