题目内容
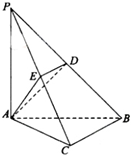 如图,在三棱锥P-ABC中,PA⊥AC,PA⊥AB,PA=AB,∠ABC=
如图,在三棱锥P-ABC中,PA⊥AC,PA⊥AB,PA=AB,∠ABC=| π |
| 3 |
| π |
| 2 |
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值.
分析:解法一:(1)先利用PA⊥AC,PA⊥AB,AC∩AB=A证得PA⊥底面ABC?PA⊥BC;再结合∠BCA=90°,即可证得BC⊥平面PAC;
(2)先利用D为PB的中点?DE∥BC?DE⊥平面PAC,得到∠DAE是AD与平面PAC所成的角;然后在Rt△ADE中求出任意两边长即可得到AD与平面PAC所成的角的正弦值.
解法二:先建立以A为原点建立空间直角坐标系A-xyz,设PA=a.求出对应各点的坐标;
(1)求出
=(0,0,a),
=(
a,0,0),得到BC⊥AP;再结合∠BCA=90°,即可证得BC⊥平面PAC;
(2)先利用D为PB的中点?DE∥BC?DE⊥平面PAC,得到∠DAE是AD与平面PAC所成的角;然后求出夹∠DAE两边的向量坐标,代入向量的数量积计算公式,求出cos∠DAE;再根据同角的正余弦之间的关系即可得到结论.
(2)先利用D为PB的中点?DE∥BC?DE⊥平面PAC,得到∠DAE是AD与平面PAC所成的角;然后在Rt△ADE中求出任意两边长即可得到AD与平面PAC所成的角的正弦值.
解法二:先建立以A为原点建立空间直角坐标系A-xyz,设PA=a.求出对应各点的坐标;
(1)求出
| AP |
| BC |
| 1 |
| 2 |
(2)先利用D为PB的中点?DE∥BC?DE⊥平面PAC,得到∠DAE是AD与平面PAC所成的角;然后求出夹∠DAE两边的向量坐标,代入向量的数量积计算公式,求出cos∠DAE;再根据同角的正余弦之间的关系即可得到结论.
解答:解:(解法一):(1)∵PA⊥AC,PA⊥AB,AC∩AB=A,
∴PA⊥底面ABC,
∴PA⊥BC.又∠BCA=90°,
∴AC⊥BC.
∴BC⊥平面PAC.(4分)
(2)∵D为PB的中点,DE∥BC,
∴DE=
BC,
又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,
∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,
∴AD=
AB,
∴在Rt△ABC中,∠ABC=60°,
∴BC=
AB.
∴在Rt△ADE中,sin∠DAE=
=
=
,
∴AD与平面PAC所成的角的正弦值是
.(12分)
(解法二):如图,以A为原点建立空间直角坐标系A-xyz,设PA=a,
由已知可得P(0,0,a),A(0,0,0),B(-
a,
a,0),C(0,
a,0).
(1)∵
=(0,0,a),
=(
a,0,0),
∴
•
=0,
∴BC⊥AP.
又∵∠BCA=90°,
∴BC⊥AC,
∴BC⊥平面PAC.(4分)
(2)∵D为PB的中点,DE∥BC,
∴E为PC的中点,
∴D(-
a,
a,
a),E(0,
a,
a),
∴又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵
=(-
a,
a,
a),
=(0,
a,
a),
∴cos∠DAE=
=
,sin∠DAE=
=
.
∴AD与平面PAC所成的角的正弦值为
.(12分)
∴PA⊥底面ABC,
∴PA⊥BC.又∠BCA=90°,
∴AC⊥BC.
∴BC⊥平面PAC.(4分)
(2)∵D为PB的中点,DE∥BC,
∴DE=
| 1 |
| 2 |
又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,
∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,
∴AD=
| 1 | ||
|
∴在Rt△ABC中,∠ABC=60°,
∴BC=
| 1 |
| 2 |
∴在Rt△ADE中,sin∠DAE=
| DE |
| AD |
| BC |
| 2AD |
| ||
| 4 |
∴AD与平面PAC所成的角的正弦值是
| ||
| 4 |
(解法二):如图,以A为原点建立空间直角坐标系A-xyz,设PA=a,
由已知可得P(0,0,a),A(0,0,0),B(-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(1)∵
| AP |
| BC |
| 1 |
| 2 |
∴
| AP |
| BC |
∴BC⊥AP.
又∵∠BCA=90°,
∴BC⊥AC,
∴BC⊥平面PAC.(4分)
(2)∵D为PB的中点,DE∥BC,
∴E为PC的中点,
∴D(-
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
∴又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵
| AD |
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| AE |
| ||
| 4 |
| 1 |
| 2 |
∴cos∠DAE=
| ||||
|
|
| ||
| 4 |
1-(
|
| ||
| 4 |
∴AD与平面PAC所成的角的正弦值为
| ||
| 4 |
点评:本题主要考查空间几何体中的位置关系、线面所成的角等知识,考查空间想象能力以及利用向量法研究空间的位置关系以及线面角问题的能力.

练习册系列答案
相关题目
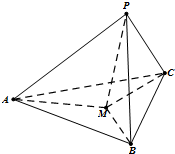 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是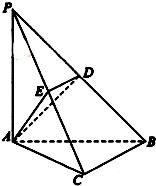 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱