题目内容
已知
，若向量
与向量
共线，则实数λ= ．
【答案】分析：根据所给的两个向量的坐标，写出
的坐标，根据两个向量之间的共线关系，写出两个向量的坐标之间的关系，得到关于λ的方程，解方程即可．
解答：解：∵
∴
=（λ+1，1）
∵向量
与向量
共线，
∴2（λ+1）-6=0
∴λ=2
故答案为：2
点评：本题考查平面向量共线的坐标表示，本题解题的关键是写出向量共线的坐标关系式，利用方程思想来解题．
的坐标，根据两个向量之间的共线关系，写出两个向量的坐标之间的关系，得到关于λ的方程，解方程即可．解答：解：∵
∴
=（λ+1，1）∵向量
与向量共线，∴2（λ+1）-6=0
∴λ=2
故答案为：2
点评：本题考查平面向量共线的坐标表示，本题解题的关键是写出向量共线的坐标关系式，利用方程思想来解题．
练习册系列答案
相关题目
，若向量
与向量
共线，则
的最大值为（ ）
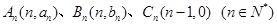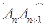，满足向量
与向量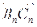
共线，且点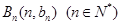
都在斜率为6的同一条直线上。若
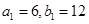。求(1)数列
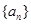的通项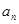
(2)数列{
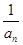}的前n项和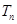
为坐标原点，则
、
、
三点在同一直线上的等价条件为存在唯一的实数
，使得
成立，此时称实数
关于
和
的终点共线分解系数”.若已知
、
,且向量
与向量
垂直,则 “向量
和
的终点共线分解系数”为（ ）
B．
C．
D．
为坐标原点，则
、
、
三点在同一直线上的等价条件为存在唯一的实数
，使得
成立，此时称实数
关于
和
的终点共线分解系数”.若已知
、
,且向量
与向量
垂直,则“向量
和
的终点共线分解系数”为（ ）
B．
C．
D．