Question

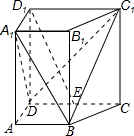如图，在直四棱柱ABCD-A₁B₁C₁D₁中，已知DC=DD₁=2AD=2AB，AD⊥DC，AB∥DC．
（Ⅰ）设E是DC的中点，求证：D₁E∥平面A₁BD；
（Ⅱ）求二面角A₁-BD-C₁的余弦值．

Answer 1

分析：（1）由题意及图形所给的线段大小之间的关系，利用线线平行进而得到线面平行；
（2）利用图形中两两垂直的线和题中所给的线段的大小，建立空间直角坐标系，利用向量的知识求出二面角的大小．

解答：解：（I）连接BE，则四边形DABE为正方形，
∴BE=AD=A₁D₁，且BE∥AD∥A₁D₁，
∴四边形A₁D₁EB为平行四边形，∴D₁E∥A₁B．
∵D₁E?平面A₁BD，A₁B?平面A₁BD，
∴D₁E∥平面A₁BD．
（II）以D为原点，DA，DC，DD₁所在直线分别为x轴、y轴、z轴，建立空间直角坐标系，
不妨设DA=1，则D（0，0，0），A（1，0，0），B（1，1，0），C₁（0，2，2），A₁（1，0，2）．
∴

DA1

=(1，0，2)，

DB

=(1，1，0)．
设

n

=(x，y，z)为平面A₁BD的一个法向量，
由

n

⊥

DA1

，

n

⊥

DB

得

x+2z=0 x+y=0

取z=1，则

n

=(-2，2，1)
设

m

=(x1，y1，z1)为平面C₁BD的一个法向量，
由

m

⊥

DC

，

m

⊥

DB

得

2y1+2z1=0 x1+y1=0

，
取z₁=1，则

m

=(1，-1，1)
∵.cos＜

m

，

n

＞=

m • n

| m || n |

=

-3

9 • 3

=-

3

3

．
由于该二面角A₁-BD-C₁为锐角，
所以所求的二面角A₁-BD-C₁的余弦值为

3

3

．

点评：此题重点考查了学生的空间想象能力，还考查了线面平行的判定定理及利用空间直角坐标系即向量的知识求二面角的大小．