题目内容
已知实数x、y满足x2+y2+2x-23y=0,求x+y的最小值.
x+y的最小值为
-1-2
.
解析:
原方程为(x+1)2+(y-3)2=4,它表示一个圆的方程,可设其参数方程为
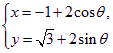(θ为参数,0≤θ<2π),
则x+y=-1+2(sinθ+cosθ)
=-1+2sin(θ+
).
当θ=
时,即x=-1-,y=-时,x+y的最小值为-1-2.
练习册系列答案
相关题目
已知实数x，y满足
-
=1(a＞0，b＞0)，则下列不等式中恒成立的是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|＜
| ||
B、y＞-
| ||
C、|y|＞-
| ||
D、y＜
|