题目内容
在某地的奥运火炬传递活动中，有编号为1，2，3，…，18的18名火炬手.若从中任选3人，则选出的火炬手的编号能组成以3为公差的等差数列的概率为（ ）
A． | B． | C． | D． |
D
解析试题分析：基本事件总数为
=17×16×3，选出火炬编号为
，当n=1时，由1,4,7,10,13,16可得4种选法；当n=2时，由2,5,8,11,14,17可得4种选法；当n=3时，由3,6,9,12,15,18可得4种选法；根据分类计算原理可得共有12种选法，所以，所求概率为P=
，故选D.
考点：古典概型.
练习册系列答案
相关题目
从装有
只红球和只黒球的口袋内任取个球，那么互斥而不对立的两个事件是( )
| A．至少有一个黒球与都是黒球 | B．至少有一个黒球与都是红球 |
C．至少有一个黒球与至少有 只红球 | D．恰有只黒球与恰有只黒球 |
从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是( )
| A．“至少有一个黑球”与“都是黑球” |
| B．“至少有一个黑球”与“都是红球” |
| C．“至少有一个黑球”与“至少有一个红球” |
| D．“恰有一个黑球”与“恰有两个黑球” |
连续抛掷两次骰子，得到的点数分别为m,n，记向量
的夹角为
，则
的概率是（ ）
A． | B． | C． | D． |
，若从区间
内随机选取一个实数
,则所选取的实数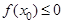
的概率为 （ ）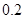
，乙命中目标的概率是
，丙命中目标的概率是
.现在三人同时射击目标，则目标被击中的概率为( )．
； 
； 
； 
.