题目内容
【题目】已知函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() ,且
,且![]() ,记点
,记点![]() ,
, ![]() .
.
(Ⅰ)求直线![]() 的方程;
的方程;
(Ⅱ)证明:线段![]() 与曲线
与曲线![]() 有且只有一个异于
有且只有一个异于![]() 、
、![]() 的公共点.
的公共点.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】【试题分析】(1)先求函数的极值点,再求两极值点的坐标,运用直线的点斜式方程求出其方程;(2)依据题设条件先构造函数将问题进行等价转化,再借助导数的知识分析推证:
(Ⅰ)令![]() ,解得
,解得![]() 或
或![]() ,
,
且![]() 在区间
在区间![]() ,
, ![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,即
,即![]() ,
, ![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为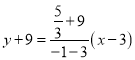 ,化简得
,化简得![]() .
.
(Ⅱ)设![]()
![]()
![]()
![]() ,
,
则线段![]() 与曲线
与曲线![]() 的公共点即
的公共点即![]() 在区间
在区间![]() 上的零点.
上的零点.
令![]()
![]() ,解得
,解得![]() ,
, ![]() ,
,
且![]() 在区间
在区间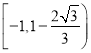 ,
, 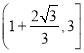 上单调递增,在区间
上单调递增,在区间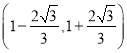 上单调递减.
上单调递减.
![]() 由
由![]()
![]() 可得
可得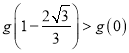
![]()
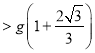 ,
,
即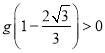 ,
, 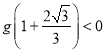 ,
,
![]() 在区间
在区间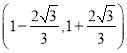 上有且仅有有一个零点.
上有且仅有有一个零点.
当![]() 时,有
时,有![]() ,
, ![]() 在
在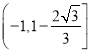 上无零点;
上无零点;
当![]() 时,有
时,有![]() ,
, ![]() 在
在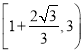 上无零点;
上无零点;
综上, ![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
所以线段![]() 与曲线
与曲线![]() 有且只有一个异于
有且只有一个异于![]() 、
、![]() 的公共点.
的公共点.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目