题目内容
在数列{an}与{bn}中,a1=1,b1=4,数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0,2an+1为bn与bn+1的等比中项,n∈N+.
(1)求a2,b2的值;
(2)求数列{an}与{bn}的通项公式.
解:(1)∵数列{an}与{bn}中,a1=1,b1=4,nSn+1-(n+3)Sn=0,
∴a1+a2-4a1=0,a1=1,解得a2=3.
∵2an+1为bn与bn+1的等比中项,
∴4a2=b2b1,b1=4,解得b2=9.
(2)由题设nSn+1-(n+3)Sn=0,a1=1,b1=4,及a2=3,b2=9,
进一步可得a3=6,b3=16,a4=10,b4=25,
由此猜想an= ,bn=(n+1)2,n∈N+.
,bn=(n+1)2,n∈N+.
先证an= ,n∈N+.
,n∈N+.
当n=1时,a1=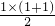 ,等式成立.
,等式成立.
当n≥2时用数学归纳法证明如下:
当n=2时,a2=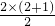 ,等式成立.
,等式成立.
假设n=k时等式成立,即ak= ,k≥2.
,k≥2.
由题设,kSk+1=(k+3)Sk,①
(k-1)Sk=(k+2)Sk-1.②
①的两边分别减去②的两边,整理得kak+1=(k+2)ak,
从而ak+1=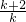 ak=
ak=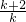 •
•
=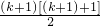 .
.
这就是说,当n=k+1时等式也成立.
综上可知,等式an= 对任何的n∈N+都成立.
对任何的n∈N+都成立.
再证bn=(n+1)2,n∈N+,
当n=1时,b1=4,∴等式成立.
假设n=k时,等式成立,即bk=(k+1)2,
那么n=k+1时,
∵(2ak+1)2=bk•bk+1,
∴[2• ]2=(k+1)2•bk+1.
]2=(k+1)2•bk+1.
∴bk+1=(k+2)2=[(k+1)+1]2.
∴n=k+1时等式成立.
∴综上知,bn=(n+1)2,n∈N+.
分析:(1)由数列{an}与{bn}中,a1=1,b1=4,nSn+1-(n+3)Sn=0,知a1+a2-4a1=0,a1=1,由2an+1为bn与bn+1的等比中项,知4a2=b2b1,b1=4,由此能求出a2,b2的值.
(2)由题设nSn+1-(n+3)Sn=0,a1=1,b1=4,及a2=3,b2=9,进一步可得a3=6,b3=16,a4=10,b4=25,由此猜想an= ,bn=(n+1)2,n∈N+.先证an=
,bn=(n+1)2,n∈N+.先证an= ,n∈N+.再证bn=(n+1)2,n∈N+.
,n∈N+.再证bn=(n+1)2,n∈N+.
点评:本题考查数列中某一项的求法,考查数列的通项公式的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化,注意合理地进行猜想和数学归纳法的合理运用.
∴a1+a2-4a1=0,a1=1,解得a2=3.
∵2an+1为bn与bn+1的等比中项,
∴4a2=b2b1,b1=4,解得b2=9.
(2)由题设nSn+1-(n+3)Sn=0,a1=1,b1=4,及a2=3,b2=9,
进一步可得a3=6,b3=16,a4=10,b4=25,
由此猜想an=
 ,bn=(n+1)2,n∈N+.
,bn=(n+1)2,n∈N+.先证an=
 ,n∈N+.
,n∈N+.当n=1时,a1=
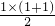 ,等式成立.
,等式成立.当n≥2时用数学归纳法证明如下:
当n=2时,a2=
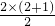 ,等式成立.
,等式成立.假设n=k时等式成立,即ak=
 ,k≥2.
,k≥2.由题设,kSk+1=(k+3)Sk,①
(k-1)Sk=(k+2)Sk-1.②
①的两边分别减去②的两边,整理得kak+1=(k+2)ak,
从而ak+1=
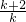 ak=
ak=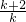 •
•
=
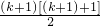 .
.这就是说,当n=k+1时等式也成立.
综上可知,等式an=
 对任何的n∈N+都成立.
对任何的n∈N+都成立.再证bn=(n+1)2,n∈N+,
当n=1时,b1=4,∴等式成立.
假设n=k时,等式成立,即bk=(k+1)2,
那么n=k+1时,
∵(2ak+1)2=bk•bk+1,
∴[2•
 ]2=(k+1)2•bk+1.
]2=(k+1)2•bk+1.∴bk+1=(k+2)2=[(k+1)+1]2.
∴n=k+1时等式成立.
∴综上知,bn=(n+1)2,n∈N+.
分析:(1)由数列{an}与{bn}中,a1=1,b1=4,nSn+1-(n+3)Sn=0,知a1+a2-4a1=0,a1=1,由2an+1为bn与bn+1的等比中项,知4a2=b2b1,b1=4,由此能求出a2,b2的值.
(2)由题设nSn+1-(n+3)Sn=0,a1=1,b1=4,及a2=3,b2=9,进一步可得a3=6,b3=16,a4=10,b4=25,由此猜想an=
 ,bn=(n+1)2,n∈N+.先证an=
,bn=(n+1)2,n∈N+.先证an= ,n∈N+.再证bn=(n+1)2,n∈N+.
,n∈N+.再证bn=(n+1)2,n∈N+.点评:本题考查数列中某一项的求法,考查数列的通项公式的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化,注意合理地进行猜想和数学归纳法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面几种推理过程是演绎推理的是( )
| A、某校高三1班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人 | ||||
| B、两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° | ||||
| C、由平面三角形的性质,推测空间四面体性质 | ||||
D、在数列{an}中a1=1,an=
|
下面几种推理过程是演绎推理的是( )
| A、两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° | ||||
| B、某校高二(1)班有55人,高二(2)班有52人,由此得高二所有班人数超过50人 | ||||
| C、由平面三角形的性质,推出空间四边形的性质 | ||||
D、在数列{an}中,a1=1,an=
|