题目内容

盒中装有7个零件，其中2个是使用过的，另外5个未经使用．
（Ⅰ）从盒中每次随机抽取1个零件，每次观察后都将零件放回盒中，求3次抽取中恰有1次抽到使用过的零件的概率；
（Ⅱ）（理）从盒中随机抽取2个零件，使用后放回盒中，记此时盒中使用过的零件个数为X，求X的分布列和数学期望．
（Ⅱ）（文）从盒中随机抽取2个零件，使用后放回盒中，求此时盒中使用过的零件个数为3或4概率．

解：（Ⅰ）记“从盒中随机抽取1个零件，抽到的是使用过的零件”为事件A，则 $\text{[math]}$ ．
所以3次抽取中恰有1次抽到使用过的零件的概率 $\text{[math]}$ ．…（6分）
（Ⅱ）（理）随机变量X的所有取值为2，3，4．
$\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ．…（8分）
所以，随机变量X的分布列为：

X	2	3	4
P	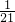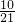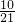$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

$\text{[math]}$ ． …（12分）
（Ⅱ）（文）∵ $\text{[math]}$ ； $\text{[math]}$ ．
∴ $\text{[math]}$ ． …（12分）
分析：（Ⅰ）先求出事件从盒中随机抽取1个零件，抽到的是使用过的零件的概率，再求3次抽取中恰有1次抽到使用过的零件的概率；
（Ⅱ）（理）确定随机变量X可取值2，3，4，求出它们的概率，然后根据期望公式求解即可得到答案；
（Ⅱ）（文）求出X=3或4的概率，即可得到此时盒中使用过的零件个数为3或4概率．
点评：本题考查离散型随机变量的分布列与期望，考查概率的计算，属于中档题．