��Ŀ����
����Ŀ������fn��x��=xn+bx+c��n��Z��b��c��R����
��1����n=��1����f��1��1��=f��1�� ![]() ��=4������ʵ��b��c��ֵ��
��=4������ʵ��b��c��ֵ��
��2����n=2����������x1 �� x2��[��1��1]��|f2��x1����f2��x2��|��4���������b��ȡֵ��Χ��
��3����n=1ʱ����֪bx2+cx��a=0����g��x��= ![]() ���Ƿ��������a��ʹ�ö�������
���Ƿ��������a��ʹ�ö������� ![]() �ϵ���������ʵ��m��n��p����������f1��g��m������f1��g��n������f1��g��p����Ϊ�߳��������Σ������ڣ����a��ȡֵ��Χ���������ڣ���˵�����ɣ�
�ϵ���������ʵ��m��n��p����������f1��g��m������f1��g��n������f1��g��p����Ϊ�߳��������Σ������ڣ����a��ȡֵ��Χ���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺n=��1���� ![]() ��
��
�ɵ�1+b+c=4��2+ ![]() b+c=4�����b=2��c=1��
b+c=4�����b=2��c=1��
��2���⣺��n=2ʱ��f2��x��=x2+bx+c��
������x1��x2��[��1��1]��|f2��x1����f2��x2��|��4������ȼ���
f2��x����[��1��1]�ϵ����ֵ����Сֵ֮��M��4��
�ٵ��� ![]() ����1����b��2ʱ��f2��x����[��1��1]������
����1����b��2ʱ��f2��x����[��1��1]������
f2��x��min=f2����1��=1��b+c��f2��x��max=f2��1��=1+b+c��
M=2b��4����ȥ����
�ڵ���1�ܩ� ![]() ��0����0��b��2ʱ��f2��x����[��1����
��0����0��b��2ʱ��f2��x����[��1���� ![]() ]�ݼ����ڣ���
]�ݼ����ڣ��� ![]() ��1]������
��1]������
f2��x��min=f2���� ![]() ��=c��
��=c�� ![]() ��f2��x��max=f2��1��=1+b+c��M=��
��f2��x��max=f2��1��=1+b+c��M=�� ![]() +1��2��4���������0��b��2��
+1��2��4���������0��b��2��
�۵�0���� ![]() ��1����2��b��0ʱ��f2��x����[��1����
��1����2��b��0ʱ��f2��x����[��1���� ![]() ]�ݼ����ڣ���
]�ݼ����ڣ��� ![]() ��1]������
��1]������
f2��x��min=f2���� ![]() ��=c��
��=c�� ![]() ��f2��x��max=f2����1��=1��b+c��M=��
��f2��x��max=f2����1��=1��b+c��M=�� ![]() ��1��2��4��������ʩ�2��b��0��
��1��2��4��������ʩ�2��b��0��
�ܵ��� ![]() ��1����b����2ʱ��f2��x����[��1��1]�ݼ���
��1����b����2ʱ��f2��x����[��1��1]�ݼ���
f2��x��min=f2��1��=1+b+c��f2��x��max=f2����1��=1��b+c��
M=��2b��4ì�ܣ�
���Ͽɵã�b��ȡֵ��Χ�ǩ�2��b��2��
��3���⣺��t=g��x��= ![]() =
= ![]() =
= ![]() ��
��
��x�� 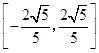 ���ɵ�t��[
���ɵ�t��[ ![]() ��1]��
��1]��
��y=t+ ![]() ��[
��[ ![]() ��1]�Ϻ���2ymin��ymax��
��1]�Ϻ���2ymin��ymax��
�ٵ�a�ʣ�0�� ![]() ]ʱ��y=t+
]ʱ��y=t+ ![]() ��[
��[ ![]() ��1]�ϵ�����
��1]�ϵ�����
ymin= ![]() +3a��ymax=a+1����2ymin��ymax��
+3a��ymax=a+1����2ymin��ymax��
��a�� ![]() ������
������ ![]() ��a��
��a�� ![]() ��
��
�ڵ�a�ʣ� ![]() ��
�� ![]() ]ʱ��y=t+
]ʱ��y=t+ ![]() ��[
��[ ![]() ��
�� ![]() ���ݼ�����
���ݼ����� ![]() ��1��������
��1��������
�ɵ�ymin=2 ![]() ��ymax=max{3a+
��ymax=max{3a+ ![]() ��a+1}=a+1����2ymin��ymax��
��a+1}=a+1����2ymin��ymax��
���7��4 ![]() ��a��7+4
��a��7+4 ![]() ������
������ ![]() ��a��
��a�� ![]() ��
��
�۵�a�ʣ� ![]() ��1��ʱ��y=t+
��1��ʱ��y=t+ ![]() ��[
��[ ![]() ��
�� ![]() ���ݼ�����
���ݼ����� ![]() ��1��������
��1��������
�ɵ�ymin=2 ![]() ��ymax=max{3a+
��ymax=max{3a+ ![]() ��a+1}=3a+
��a+1}=3a+ ![]() ����2ymin��ymax��
����2ymin��ymax��
��� ![]() ��a��
��a�� ![]() ������
������ ![]() ��a��1��
��a��1��
�ܵ�a��[1��+�ޣ�ʱ��y=t+ ![]() ��[
��[ ![]() ��1]�ϵݼ���
��1]�ϵݼ���
ymin=a+1��ymax=3a+ ![]() ����2ymin��ymax��
����2ymin��ymax��
��a�� ![]() ������1��a��
������1��a�� ![]() ��
��
���Ͽɵã����������������Σ�a��ȡֵ��Χ�� ![]() ��a��
��a�� ![]() ��
��
����������1�����������ɵ�b��c�ķ��̣��ⷽ�̿ɵ�b��c����2����n=2ʱ��f2��x��=x2+bx+c��������x1��x2��[��1��1]��|f2��x1����f2��x2��|��4������ȼ���f2��x����[��1��1]�ϵ����ֵ����Сֵ֮��M��4�����۶Գ��������Ĺ�ϵ���жϵ����ԣ��ɵ���ֵ���ⲻ��ʽ���ɵõ�����Χ����3����t=g��x��= ![]() =
= ![]() =
= ![]() ����x��
����x�� ![]() ���ɵ�t��[
���ɵ�t��[ ![]() ��1]����y=t+
��1]����y=t+ ![]() ��[
��[ ![]() ��1]�Ϻ���2ymin��ymax�����۶��㴦x=
��1]�Ϻ���2ymin��ymax�����۶��㴦x= ![]() ������[
������[ ![]() ��1]�Ĺ�ϵ����õ����ԣ��ɵ���ֵ���ⲻ��ʽ���ɵõ����ڣ����a�ķ�Χ��
��1]�Ĺ�ϵ����õ����ԣ��ɵ���ֵ���ⲻ��ʽ���ɵõ����ڣ����a�ķ�Χ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ijУ100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]�� 
��1����ͼ��a��ֵ��
��2������Ƶ�ʷֲ�ֱ��ͼ��������100��ѧ�����ijɼ���ƽ���֣�
��3������100��ѧ�����ijɼ�ijЩ�����ε�������x������ѧ�ɼ���Ӧ�����ε�������y��֮�������ʾ������ѧ�ɼ���[50��90��֮���������
������ | [50��60�� | [60��70�� | [70��80�� | [80��90�� |
x��y | 1��1 | 2��1 | 3��4 | 4��5 |

