题目内容
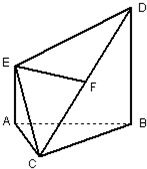 如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD中点.
如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD中点.(1)求证:EF∥平面ABC;(2)求证:EF⊥平面BCD.
分析:(1)取BC中点O,连接OF,可证四边形EAOF是平行四边形,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(2)连接BF,由EF2+BF2=BE2得到BF⊥EF,又EF⊥CD,则线面垂直的判断定理证明.
(2)连接BF,由EF2+BF2=BE2得到BF⊥EF,又EF⊥CD,则线面垂直的判断定理证明.
解答:解::(1)证明:取BC中点O,连接OF
∵F是CD中点,O为CB中点,∴OF∥DB且OF=
DB,
又BD∥AE且AE=
BD
∴OF∥AE,OF=AE
∴四边形EAOF是平行四边形
∴OA∥FE
又∵OA?平面ABC,EF?平面ABC
∴EF∥平面ABC.
(2)连接BF,∵AE=1,则AB=BC=AC=BD=2,
于是 CE=ED=
,CD=2
,
所以 EF=
,BF=
,BE=
所以BF⊥EF,又EF⊥CD,又BF,CD为两条相交直线
故EF⊥平面BCD
∵F是CD中点,O为CB中点,∴OF∥DB且OF=
| 1 |
| 2 |
又BD∥AE且AE=
| 1 |
| 2 |
∴OF∥AE,OF=AE
∴四边形EAOF是平行四边形
∴OA∥FE
又∵OA?平面ABC,EF?平面ABC
∴EF∥平面ABC.
(2)连接BF,∵AE=1,则AB=BC=AC=BD=2,
于是 CE=ED=
| 5 |
| 2 |
所以 EF=
| 3 |
| 2 |
| 5 |
所以BF⊥EF,又EF⊥CD,又BF,CD为两条相交直线
故EF⊥平面BCD
点评:考查空间想象能力、逻辑思维能力、运算求解能力和探究能力,同时考查学生灵活利用图形,借助向量工具解决问题的能力,考查数形结合思想.是中档题.

练习册系列答案
相关题目
 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC, (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=