题目内容
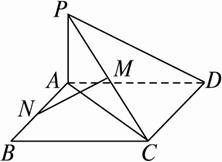
如图，四边形ABCD为矩形，PA⊥平面ABCD，PA=AD，M、N分别是PC、AB的中点.求证：MN⊥平面PCD.
思路分析：证明线面垂直，需要证明线与平面内两条相交直线垂直，即转化为线线的垂直，非零空间向量的数量积为零可以解决线线垂直的关系.
证明:设
=a,
=b,
=c,则{a,b,c}为空间的一个基底.
则
=
(a+b+c)=
(a+c).
∵
=b,
=c-a,PA⊥矩形ABCD，
∴PA⊥AB，PA⊥AD.
且AB⊥AD.
∴a·b=0,b·c=0,c·a=0.
故
·
=
(a+c)·b=
(a·b+c·b)=0,
·
=
(a+c)·(c-a)=
(|c|2-|a|2)=
(|
|2-|
|2)=0.
∴MN⊥DC,MN⊥PD.
又DC∩PD=D，
∴MN⊥平面PCD.
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=