题目内容
已知O是正三角形ABC内部一点，满足
+2
+4
=
，则
=（ ）
| OA |
| OB |
| OC |
| 0 |
| S△AOB |
| S△AOC |
分析：作出正△ABC，并延长OC到D，使
=4
，延长OB到E，使
=2
．可得S△AOC=
S△AOD，同理S△AOB=
S△AOE，因为△AOE的面积与△AOD的面积都等于平行四边形OEFD面积的一半，所以S△AOC=
S△AOB，可得
=2．
| OD |
| OC |
| OE |
| OB |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| S△AOB |
| S△AOC |
解答：解：∵
+2
+4
=
，∴-
=2
+4
延长OC到D，使
=4
，延长OB到E，使
=2
以OD、OE为邻边作平行四边形OEFD，可得
=
+
∴
、
互为相反向量，得O为AF的中点
∵△AOD中，
=
，
∴△AOC的面积S△AOC=
S△AOD，同理可得S△AOB=
S△AOE
∵S△AOD=S△AOE=
S平行四边形OEFD，
∴S△AOC=
S△AOB，可得
=2
故选：C
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
延长OC到D，使
| OD |
| OC |
| OE |
| OB |
以OD、OE为邻边作平行四边形OEFD，可得
| OF |
| OD |
| OE |
∴
| OA |
| OF |
∵△AOD中，
| OC |
| 1 |
| 4 |
| OD |
∴△AOC的面积S△AOC=
| 1 |
| 4 |
| 1 |
| 2 |
∵S△AOD=S△AOE=
| 1 |
| 2 |
∴S△AOC=
| 1 |
| 2 |
| S△AOB |
| S△AOC |
故选：C
点评：本题给出正三角形ABC内部一点O满足特殊的向量等式，求两个小三角形的面积比．着重考查了平面向量的线性运算和向量在几何中的应用等知识点，属于中档题．
练习册系列答案
相关题目
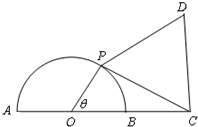如图，已知⊙O的半径为1，点C在直径AB的延长线上，BC=1，点P是半圆上的一个动点，以PC为边作正三角形PCD，且点D与圆心分别在PC两侧．
已知△OAB是边长为4的正三角形，CO⊥平面OAB，且CO=2，设D、E分别是OA、AB的中点．
